(本题满分15分)已知a∈R，函数f (x) =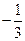
x3 + 
ax2 + 2ax (x∈R)． （Ⅰ）当a = 1时，求函数f (x)的单调递增区间； （Ⅱ）函数f (x) 能否在R上单调递减，若是，求出a的取值范围；若不能，请说明理由； （Ⅲ）若函数f (x)在[-1，1]上单调递增，求a的取值范围．
有一个3×3×3的正方体, 它的六个面上均涂上颜色. 现将这个长方体锯成27个1×1×1的小正方体，从这些小正方体中随机地任取1个.
如每次从中任取一个小正方体，确定涂色的面数后，再放回，连续抽取6次，设恰好取到只有一个面涂有颜色的小正方体的次数为
. 求的数学期望.
已知函数
（I）设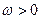
为常数，若
上是增函数，求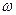
的取值范围
（II）若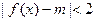
成立的充分条件是
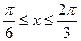，求实数m的取值范围
（1）求实数
的值；
（2）求函数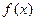
的图象与
轴公共点的个数；
（3）
，使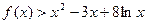
成立，求实数
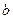的取值范围.（参考数据：
，
）
（1）若离心率为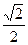
，求椭圆的方程；
（2）当
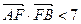时，求椭圆离心率的取值范围
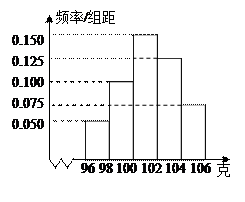
（1）求样本中产品净重小于100克的频率；
（2）已知样本中产品净重小于100克的件数是72，求样本中净重（单位：克）在[100，104)范围内的件数；
（3）若这批产品共有10000件，试估计其中净重（单位：克）在[104，106] 范围内的件数.