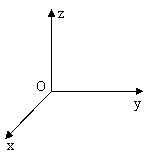
空间存在着以x=0平面为分界面的两个匀强磁场,左右两边磁场的磁感应强度分别为B1和B2,且B1:B2=4:3,方向如图所示。现在原点O处一静止的中性原子,突然分裂成两个带电粒子a和b,已知a带正电荷,分裂时初速度方向为沿x轴正方向,若a粒子在第四次经过y轴时,恰好与b粒子第一次相遇。求:
a粒子在磁场B1中作圆周运动的半径与b粒子在磁场B2中圆周运动的半径之比。
|
a粒子和b粒子的质量之比。
某实验室工作人员,用初速度v0=0.09C(C为真空中的光速)的 粒子,轰击静止的氮原子核
粒子,轰击静止的氮原子核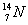 ,产生了质子
,产生了质子 .若某次碰撞可看作对心正碰,碰后新核与质子同方向运动,垂直磁场方向射入磁场,通过分析偏转半径可得出新核与质子的速度大小之比为1:20,已知质子质量为m。
.若某次碰撞可看作对心正碰,碰后新核与质子同方向运动,垂直磁场方向射入磁场,通过分析偏转半径可得出新核与质子的速度大小之比为1:20,已知质子质量为m。
①写出核反应方程
②求出质子的速度v
③若用上述两个质子发生对心弹性碰撞,则每个质子的动量变化量是多少?(保留两位有效数字)
质量为m1=1.0kg和m2(未知)的两个物体在光滑的水平面上正碰,碰撞时间不计,其χ-t (位移-时间) 图象如图所示,试通过计算回答下列问题:
(1)m2等于多少千克?
(2)质量为m1的物体在碰撞过程中动量变化量是多少?
(3)碰撞过程是弹性碰撞还是非弹性碰撞?
空间中存在方向垂直于纸面向里的匀强磁场,磁感应强度为B,一带电量为+q、质量为m的粒子,在p点以某一初速开始运动,初速方向在图中纸面内如图中P点箭头所示。该粒子运动到图中Q点时速度方向与P点时速度方向垂直,如图中Q点箭头所示。已知P、Q间的距离为l。若保持粒子在P点时的速度不变,而将匀强磁场换成匀强电场,电场方向与纸面平行且与粒子在P点时速度方向垂直,在此电场作用下粒子也由P点运动到Q点。不计重力。求:
(1)电场强度的大小。
(2)两种情况中粒子由P运动到Q点所经历的时间之差。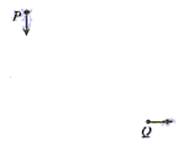
如图,一半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属板,两板间的距离为d,板长为l,t=0时,磁场的磁感应强度B从B0开始均匀增大,同时,在板2的左端且非常靠近板2的位置有一质量为m、带电量为-q的液滴以初速度v0水平向右射入两板间,该液滴可视为质点。
⑴要使该液滴能从两板间射出,磁感应强度随时间的变化率K应满足什么条件?
⑵要使该液滴能从两板间右端的中点射出,磁感应强度B与时间t应满足什么关系?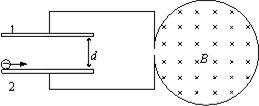
在同时存在匀强电场和匀强磁场的空间中取正交坐标系Oxyz(z轴正方向竖直向上),如图所示。已知电场方向沿z轴正方向,场强大小为E;磁场方向沿y轴正方向,磁感应强度的大小为B;重力加速度为g。问:一质量为m、带电量为+q的从原点出发的质点能否在坐标轴(x,y,z)上以速度v做匀速运动?若能,m、q、E、B、v及g应满足怎样的关系?若不能,说明理由。