(本小题满分12分)
求适合下列条件的圆锥曲线方程:
(1).长轴长是短轴长的3倍,经过点(3,0)的椭圆标准方程。
(2).已知双曲线两个焦点的坐标为 ,双曲线上一点P到两焦点的距离之差的绝对值等于6,求双曲线标准方程.
,双曲线上一点P到两焦点的距离之差的绝对值等于6,求双曲线标准方程.
(3).已知抛物线的顶点在原点,准线与其平行线x=2的距离为3,求抛物线标准方程.
求下列各式的值.
(1)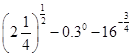 ;(2)设
;(2)设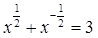 ,求
,求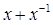 的值;
的值;
(3)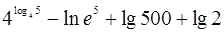 .
.
如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.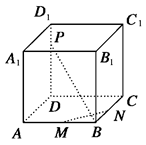
(Ⅰ)若 ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(Ⅱ)棱DD1上是否存在这样的点P,使得平面APC1⊥平面A1ACC1?证明你的结论.
如图(1)示,在梯形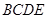 中,
中,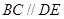 ,
, ,且
,且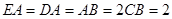 ,如图(2)沿
,如图(2)沿 将四边形
将四边形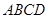 折起,使得平面
折起,使得平面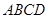 与平面
与平面 垂直,
垂直, 为
为 的中点.
的中点.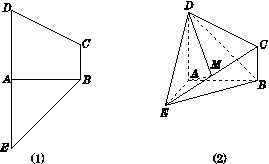
(Ⅰ)求证: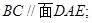
(Ⅱ)求证: ;
;
(Ⅲ)求点D到平面BCE的距离。
如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.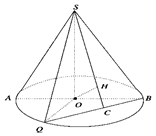
(Ⅰ)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(Ⅱ)如果∠AOQ=60°,QB=2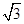 ,求此圆锥的体积和侧面积.
,求此圆锥的体积和侧面积.
一个正三棱柱的三视图如图所示,求这个正三棱柱的体积和表面积.