如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.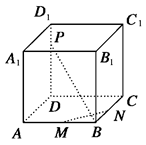
(Ⅰ)若 ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(Ⅱ)棱DD1上是否存在这样的点P,使得平面APC1⊥平面A1ACC1?证明你的结论.
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2个小题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系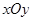 中,把矩阵
中,把矩阵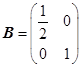 确定的压缩变换
确定的压缩变换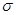 与矩阵
与矩阵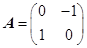 确定的旋转变换
确定的旋转变换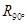 进行复合,得到复合变换
进行复合,得到复合变换 .
.
(Ⅰ)求复合变换 的坐标变换公式;
的坐标变换公式;
(Ⅱ)求圆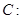
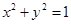 在复合变换
在复合变换 的作用下所得曲线
的作用下所得曲线 的方程.
的方程.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系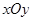 中,直线
中,直线 的参数方程为
的参数方程为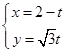 (
( 为参数),
为参数),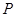 、
、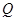 分别为直线
分别为直线 与
与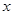 轴、
轴、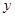 轴的交点,线段
轴的交点,线段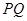 的中点为
的中点为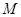 .
.
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点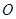 为极点,
为极点,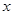 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点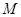 的极坐标和直线
的极坐标和直线 的极坐标方程.
的极坐标方程.
(3)(本小题满分7分)选修4—5:不等式选讲
已知不等式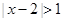 的解集与关于
的解集与关于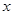 的不等式
的不等式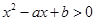 的解集相等.
的解集相等.
(Ⅰ)求实数 ,
,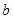 的值;
的值;
(Ⅱ)求函数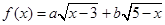 的最大值,以及取得最大值时
的最大值,以及取得最大值时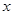 的值.
的值.
(本小题满分14分)
已知函数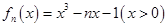 ,
, .
.
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)判断函数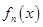 在区间
在区间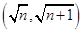 上零点的个数,并给予证明;
上零点的个数,并给予证明;
(Ⅲ)阅读右边的程序框图,请结合试题背景简要描述其算法功能,并求出执行框图所表达的算法后输出的 值.
值.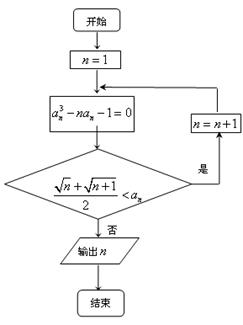
(本小题满分13分)
已知点 为抛物线
为抛物线 :
:  的焦点,
的焦点,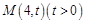 为抛物线
为抛物线 上的点,且
上的点,且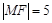 .
.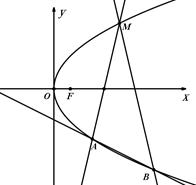
(Ⅰ)求抛物线 的方程和点
的方程和点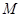 的坐标;
的坐标;
(Ⅱ)过点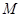 引出斜率分别为
引出斜率分别为 的两直线
的两直线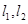 ,
,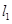 与抛物线
与抛物线 的另一交点为
的另一交点为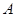 ,
,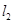 与抛物线
与抛物线 的另一交点为
的另一交点为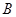 ,记直线
,记直线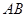 的斜率为
的斜率为 .
.
(ⅰ)若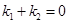 ,试求
,试求 的值;
的值;
(ⅱ)证明: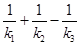 为定值.
为定值.
(本小题满分13分)
如图1,在等腰梯形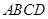 中,
中,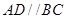 ,
,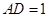 ,
,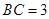 ,
,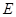 为
为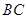 上一点,
上一点, 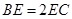 ,且
,且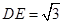 .将梯形
.将梯形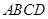 沿
沿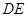 折成直二面角
折成直二面角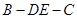 ,如图2所示.
,如图2所示.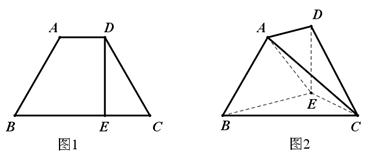
(Ⅰ)求证:平面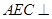 平面
平面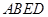 ;
;
(Ⅱ)设点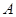 关于点
关于点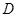 的对称点为
的对称点为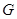 ,点
,点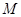 在
在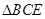 所在平面内,且直线
所在平面内,且直线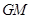 与平面
与平面 所成的角为
所成的角为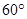 ,试求出点
,试求出点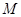 到点
到点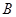 的最短距离.
的最短距离.
(本小题满分13分)
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为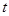 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若 ,则该零件为优等品;若
,则该零件为优等品;若 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
| 尺寸 |
 |
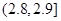 |
 |
 |
 |
 |
| 甲机床零件频数 |
2 |
3 |
20 |
20 |
4 |
1 |
| 乙机床零件频数 |
3 |
5 |
17 |
13 |
8 |
4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元. 若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式: .
.
参考数据:
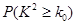 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
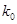 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |