(本小题满分12分)
已知抛物线以原点为顶点,以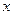 轴为对称轴,焦点在直线
轴为对称轴,焦点在直线 上.
上.
(1)求抛物线的方程;(2)设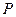 是抛物线上一点,点
是抛物线上一点,点 的坐标为
的坐标为 ,求
,求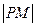 的最小值(用
的最小值(用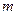 表示),并指出此时点
表示),并指出此时点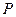 的坐标。
的坐标。
(本小题满分12分)在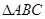 中,角
中,角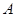 ,
,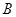 ,
,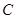 的对边分别为
的对边分别为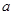 ,
,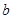 ,
,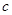 ,已知向量
,已知向量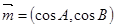 ,
,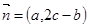 ,且
,且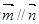 .
.
(1)求角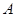 的大小;
的大小;
(2)若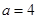 ,求
,求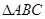 面积的最大值.
面积的最大值.
(本小题满分12分)已知二次函数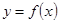 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为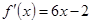 .数列
.数列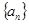 的前
的前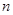 项和为
项和为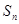 ,点
,点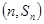
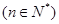 均在函数
均在函数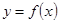 的图象上.
的图象上.
(1)求数列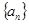 的通项公式;
的通项公式;
(2)设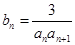 ,
,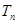 是数列
是数列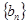 的前
的前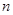 项和,求使得
项和,求使得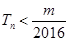 对所有
对所有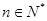 都成立的最小正整数
都成立的最小正整数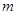 .
.
(本小题满分10分)设命题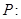 函数
函数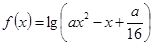 的定义域为
的定义域为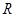 ;命题
;命题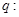 不等式
不等式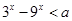 对一切正实数
对一切正实数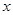 均成立..
均成立..
(1)如果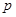 是真命题,求实数
是真命题,求实数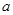 的取值范围;
的取值范围;
(2)如果命题“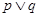 ”为真命题,且“
”为真命题,且“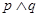 ”为假命题,求实数
”为假命题,求实数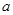 的取值范围.
的取值范围.
(本题10分) 设 是偶函数,且当
是偶函数,且当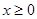 时,
时,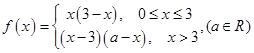 .
.
(1)当 时,求
时,求 的解析式;
的解析式;
(2)设函数 在区间
在区间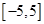 上的最大值为
上的最大值为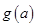 ,试求
,试求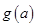 的表达式.
的表达式.
(本题10分)设 是正实数,且
是正实数,且 ,记
,记
(1)求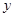 关于
关于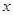 的函数关系式
的函数关系式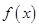 ,并求其定义域
,并求其定义域 ;
;
(2)若函数 在区间
在区间 内有意义,求实数
内有意义,求实数 的取值范围.
的取值范围.