对于下述命题 ,写出“
,写出“ ”形式的命题,并判断“
”形式的命题,并判断“ ”与“
”与“ ”的真假:
”的真假:
(1) 
 (其中全集
(其中全集 ,
, ,
, ).
).
(2)  有一个素数是偶数;.
有一个素数是偶数;.
(3)  任意正整数都是质数或合数;
任意正整数都是质数或合数;
(4)  三角形有且仅有一个外接圆.
三角形有且仅有一个外接圆.
(本小题满分12分)设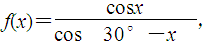 ,
,
(1)求f(x)+f(60°-x)(2)求f(1°)+f(2°)+…+f(59°)的值
.(本题满分12分)若关于x的方程x2+2ax+2-a=0有两个不相等的实根,求分别满足下列条件的a的取值范围.
(1)方程两根都小于1;
(2)方程一根大于2,另一根小于2.
(本小题满分12分)设集合A={x|x2<4},B={x|1<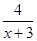 }.
}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
(本小题满分10分)(1)将形如 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 =a11a22-a12a21,试计算二阶行列式
=a11a22-a12a21,试计算二阶行列式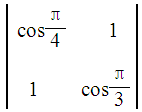 的值;
的值;
(2)已知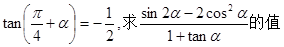 。
。
已知平面上的动点P(x,y)及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是k1,k2,且k1·k2=-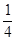 .
.
(1)求动点P的轨迹C的方程;
(2)已知直线l:y=kx+m与曲线C交于M,N两点,且直线BM、BN的斜率都存在,并满足kBM·kBN=-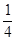 ,求证:直线l过原点.
,求证:直线l过原点.