已知平面上的动点P(x,y)及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是k1,k2,且k1·k2=-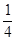 .
.
(1)求动点P的轨迹C的方程;
(2)已知直线l:y=kx+m与曲线C交于M,N两点,且直线BM、BN的斜率都存在,并满足kBM·kBN=-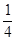 ,求证:直线l过原点.
,求证:直线l过原点.
(共12分)设集合 .
.
(1)若 ,求
,求 ;
;
(2)若 ,求实数a的范围.
,求实数a的范围.
(共10分)
(1)若 ,求
,求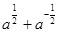 的值;
的值;
(2)已知 ,求
,求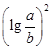 的值.
的值.
(本大题满分12分)对于在区间 上有意义的两个函数
上有意义的两个函数 与
与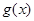 ,如果对任意的
,如果对任意的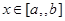 ,均有
,均有 ,则称
,则称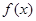 与
与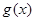 在
在 上是接近的,否则称
上是接近的,否则称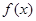 与
与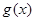 在
在 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数 与
与 ,现给定区间
,现给定区间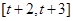 .
.
(1)若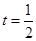 ,判断
,判断 与
与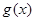 是否在给定区间上接近;
是否在给定区间上接近;
(2)若 与
与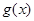 在给定区间
在给定区间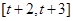 上都有意义,求
上都有意义,求 的取值的集合
的取值的集合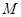 ;
;
(3)在(2)的条件下,是否存在 ,使得
,使得 与
与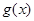 在给定区间
在给定区间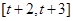 上是接近的;若存在,求
上是接近的;若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本大题满分12分)定义在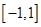 上的函数
上的函数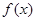 满足:①对任意
满足:①对任意 且
且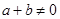 ,都有
,都有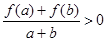 成立; ②
成立; ②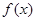 在
在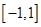 上是奇函数,且
上是奇函数,且 .
.
(1)求证: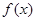 在
在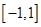 上是单调递增函数;
上是单调递增函数;
(2)解关于 不等式
不等式 ;
;
(3)若 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数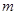 的取值范围.
的取值范围.
(本大题满分12分)如图所示,有一块半径为 的半圆形钢板,设计剪裁成矩形ABCD的形状,它的边
的半圆形钢板,设计剪裁成矩形ABCD的形状,它的边 在圆O的直径上,边CD的端点在圆周上,若设矩形的边
在圆O的直径上,边CD的端点在圆周上,若设矩形的边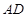 为
为 ;
;
(1)将矩形的面积 表示为关于
表示为关于 的函数,并求其定义域;
的函数,并求其定义域;
(2)求矩形面积的最大值及此时边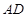 的长度.
的长度.