(本大题满分12分)定义在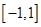 上的函数
上的函数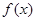 满足:①对任意
满足:①对任意 且
且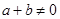 ,都有
,都有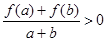 成立; ②
成立; ②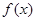 在
在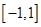 上是奇函数,且
上是奇函数,且 .
.
(1)求证: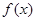 在
在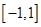 上是单调递增函数;
上是单调递增函数;
(2)解关于 不等式
不等式 ;
;
(3)若 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数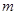 的取值范围.
的取值范围.
(本小题满分14分)已知 是函数
是函数 的一个极值点。
的一个极值点。
(Ⅰ)求 ;
;
(Ⅱ)若直线 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求 的取值范围;
的取值范围;
(Ⅲ)设 =(
=( )
) +
+ +(6-
+(6- +2(
+2( ),
), ,若
,若 =0有两个零点
=0有两个零点 ,且
,且 ,试探究
,试探究 值的符号
值的符号
(本小题满分13分)已知 、
、 ,椭圆C的方程为
,椭圆C的方程为 ,
, 、
、 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设 为椭圆C上一点,存在以
为椭圆C上一点,存在以 为圆心的
为圆心的 与
与 外切、与
外切、与 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 作斜率为
作斜率为 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与 轴相交于点D,若
轴相交于点D,若 求
求 的值;
的值;
(Ⅲ)已知真命题:“如果点T( )在椭圆
)在椭圆 上,那么过点T
上,那么过点T
的椭圆的切线方程为 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
(本小题满分13分)如图,由不大于n(n∈ )的正有理数排成的数表,质点按
)的正有理数排成的数表,质点按
 ……顺序跳动,
……顺序跳动,
所经过的有理数依次排列构成数列 。
。
(Ⅰ)质点从 出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从
出发,通过抛掷骰子来决定质点的跳动步数,骰子的点数为奇数时,质点往前跳一步(从 到达
到达 );骰子的点数为偶数时,质点往前跳二步(从
);骰子的点数为偶数时,质点往前跳二步(从 到达
到达 ).
).
①抛掷骰子二次,质点到达的有理数记为ξ,求Eξ;②求质点恰好到达 的概率。
的概率。
(Ⅱ)试给出 的值(不必写出求解过程)。
的值(不必写出求解过程)。
(本小题满分13分)如图,在正方体 的上底面上叠放三棱柱
的上底面上叠放三棱柱 ,该几何体的正视图与左视图如右图所示.
,该几何体的正视图与左视图如右图所示.
(Ⅰ)若

 ,求实数
,求实数 的值;
的值;
(Ⅱ)在(I)的条件下:
① 证明
 平面
平面 ;
;
②求直线 与平面
与平面 所成角的正弦值
所成角的正弦值

(本小题满分13分)已知向量
 ,
, ,
,
定义函数 =
= 。
。
(Ⅰ)求 的最小正周期;在所给的坐标系中作出函数
的最小正周期;在所给的坐标系中作出函数 ,
, ∈
∈ 的图象
的图象
(不要求写出作图过程);
(Ⅱ)若 =2,且14≤
=2,且14≤ ≤18,求
≤18,求 的值
的值