袋中有同样的球5个,其中3个红色,2个黄色,现从中随机且不返回地摸球,每次摸1个,当两种颜色的球都被摸到时,即停止摸球,记随机变量 为此时已摸球的次数,求:
为此时已摸球的次数,求:
(1)随机变量 的概率分布列;(2)随机变量
的概率分布列;(2)随机变量 的数学期望与方差.
的数学期望与方差.
在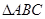 中,角
中,角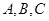 的对边分别是
的对边分别是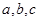 ,若
,若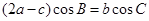 .
.
(1)求角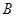 的大小;
的大小;
(2)若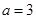 ,
,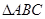 的面积为
的面积为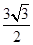 ,求
,求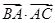 的值.
的值.
已知圆 的圆心为
的圆心为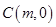 ,
,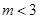 ,半径为
,半径为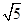 ,圆
,圆 与离心率
与离心率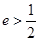 的椭圆
的椭圆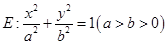 的其中一个公共点为
的其中一个公共点为 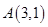 ,
,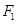 ,
,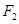 分别是椭圆的左、右焦点.
分别是椭圆的左、右焦点.
(1)求圆 的标准方程;
的标准方程;
(2)若点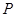 的坐标为
的坐标为 ,试探究直线
,试探究直线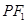 与圆
与圆 能否相切,若能,求出椭圆
能否相切,若能,求出椭圆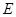 和直线
和直线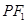 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
如图,三棱柱 中,侧棱
中,侧棱 平面
平面 ,
, 为等腰直角三角形,
为等腰直角三角形, ,且
,且 分别是
分别是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
(3)若点 是
是 上一点,求
上一点,求 的最小值.
的最小值.
设有关于 的一元二次方程
的一元二次方程 .
.
(1)若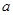 是从
是从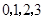 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若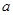 是从区间
是从区间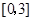 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
已知函数 (其中
(其中 ),
), .
.
(1)若命题
 是假命题,求
是假命题,求 的取值范围;
的取值范围;
(2)若命题 ,命题
,命题
 满足
满足 或
或 为真命题,若
为真命题,若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围.
的取值范围.