资料：理论分析表明，逃逸速度是环绕速度的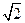
倍．即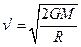
，由此可知，天体的质量M越大，半径R越小，逃逸速度也就越大，也就是说，其表面的物体就越不容易脱离它的束缚．有些恒星，在它一生的最后阶段，强大的引力把其中的物质紧紧的压在一起，密度极大，每立方米的质量可达数吨．它们的质量非常大，半径又非常小，其逃逸速度非常大．于是，我们自然要想，会不会有这样的天体，它的质量更大，半径更小，逃逸速度更大，以
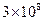m/s的速度传播的光都不能逃逸？如果宇宙中真的存在这样的天体，即使它确实在发光，光也不能进入太空，我们根本看不到它．这种天体称为黑洞(black hole)。1970年，科学家发现了第一个很可能是黑洞的目标．已知
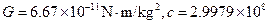m/s，求：
（1）逃逸速度大于真空中光速的天体叫黑洞（black hole)，设某黑洞的质量等于太阳的质量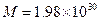
kg，求它的可能最大半径（这个半径叫做Schwarzchild半径）．
（2）在目前天文观测范围内，物质的平均密度为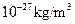
，如果认为我们的宇宙是这样一个均匀大球体，其密度使得它的逃逸速度大于光在真空中的速度c，因此任何物体都不能脱离宇宙，问宇宙的半径至少多大？（球的体积计算方程
）
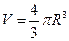如图所示是建筑工地上常用的一种“深穴打夯机”。工作时，电动机带动两个紧压夯杆的滚轮匀速转动将夯杆从深为h的坑中提上来，当两个滚轮彼此分开时，夯杆被释放，最后夯杆在自身重力的作用下落回深坑，夯实坑底；然后两个滚轮再次压紧，夯杆再次被提上来，如此周而复始工作。已知两个滚轮边缘的线速度v恒为4m/s，每个滚轮对夯杆的正压力FN =2×104 N，滚轮和夯杆间的动摩擦因数μ =" 0.3" ，夯杆的质量m =1×10 3kg，坑深h ="6.4m" 。假定在打夯的过程中坑的深度变化不大，且夯的低端升到坑口时，速度正好为零。取g =10m/s2。试求：
（1）夯杆上升的过程中，被滚轮释放时它的速度为多大？
此时夯杆低端离坑底多高？
（2）每个打夯周期中，电动机对夯杆所做的功为多少？
（3）每个打夯周期中，由于摩擦产生的热量。
（4）打夯周期T.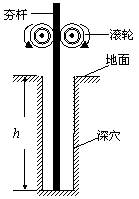
有一颗竖直向上发射的炮弹，炮弹的质量为M=6.0kg（内含炸药的质量可以忽略不计），射出的初速度v0=60m/s。当炮弹到达最高点时爆炸为沿水平方向运动的两片，其中一片质量为m=4.0kg。现要求这一片不能落到以发射点为圆心、以R=600m为半径的圆周范围内，则刚爆炸完时两弹片的总动能至少多大？（g=10/s2，忽略空气阻力）
以速度v0平抛一个质量为1kg的物体，若在抛出3s后它未与地面及其他物体相碰，求它在3s内动量的变化。
据报道，1980年一架英国战斗机在威尔士上空与一只秃鹰相站撞，飞机坠毁。小小的飞鸟撞坏庞大、坚实的飞机，真难以想象。试通过估计，说明鸟类对飞机飞行的威胁，设飞鸟的质量m=1kg，飞机的飞行速度为v="800m/s" ，若两者相撞，试估算鸟对飞机的撞击力。
把地球绕太阳公转看作是匀速圆周运动，轨道平均半径约为1.5×108km，已知万有引力常量G＝6.67×10－11N·m2/kg2，则可估算出太阳的质量大约是多少kg？（结果取一位有效数字）