如图所示是建筑工地上常用的一种“深穴打夯机”。工作时，电动机带动两个紧压夯杆的滚轮匀速转动将夯杆从深为h的坑中提上来，当两个滚轮彼此分开时，夯杆被释放，最后夯杆在自身重力的作用下落回深坑，夯实坑底；然后两个滚轮再次压紧，夯杆再次被提上来，如此周而复始工作。已知两个滚轮边缘的线速度v恒为4m/s，每个滚轮对夯杆的正压力FN =2×104 N，滚轮和夯杆间的动摩擦因数μ =" 0.3" ，夯杆的质量m =1×10 3kg，坑深h ="6.4m" 。假定在打夯的过程中坑的深度变化不大，且夯的低端升到坑口时，速度正好为零。取g =10m/s2。试求：
（1）夯杆上升的过程中，被滚轮释放时它的速度为多大？
此时夯杆低端离坑底多高？
（2）每个打夯周期中，电动机对夯杆所做的功为多少？
（3）每个打夯周期中，由于摩擦产生的热量。
（4）打夯周期T.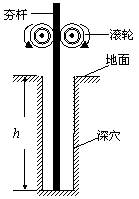
如图所示，斜面倾角为45°，从斜面上方A点处由静止释放一个质量为m的弹性小球，在B点处和斜面碰撞，碰撞后速度大小不变，方向变为水平，经过一段时间在C点再次与斜面碰撞。已知AB两点的高度差为h，重力加速度为g，不考虑空气阻力。求：
（1）小球在AB段运动过程中重力做功的平均功率P；
（2）小球落到C点时速度的大小。
为了响应国家的"节能减排"号召，某同学采用了一个家用汽车的节能方法．在符合安全行驶要求的情况下，通过减少汽车后备箱中放置的不常用物品和控制加油量等措施，使汽车负载减少．假设汽车以72 的速度匀速行驶时，负载改变前、后汽车受到的阻力分别为2 000 和1 950 ．请计算该方法使汽车发动机输出功率减少了多少？
某校物理兴趣小组决定举行遥控赛车比赛。比赛路径如图所示，赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直圆轨道，离开竖直圆轨道后继续在光滑平直轨道上运动到C点，并能越过壕沟。已知赛车质量m=0.1kg，通电后以额定功率P=1.5w工作，进入竖直轨道前受到阻力恒为0.3N，随后在运动中受到的阻力均可不记。图中L=10.00m，R=0.32m，h=1.25m，S=1.50m。问：要使赛车完成比赛，电动机至少工作多长时间？（取g="10" m/s2）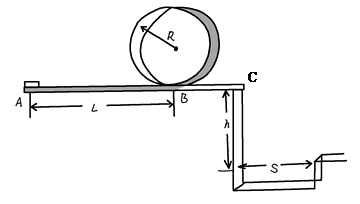
如图所示，滑块质量为m，与水平地面间的动摩擦因数为0.1，它以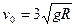
的初速度由A点开始向B点滑行，AB=5R，并滑上光滑的半径为R的
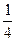圆弧BC，在C点正上方有一离C点高度也为R的旋转平台，沿平台直径方向开有两个离轴心距离相等的小孔P、Q，旋转时两孔均能达到C点的正上方。若滑块滑过C点后P孔，又恰能从Q孔落下，则平台转动的角速度ω应满足什么条件？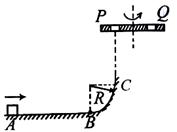
如图所示，光滑绝缘杆上套有两个完全相同、质量都是m的金属小球a、b，a带电量为q（q＞0），b不带电。M点是ON的中点，且OM=MN=L，整个装置放在与杆平行的匀强电场中。开始时，b静止在杆上MN之间的某点P处，a从杆上O点以速度v0向右运动，到达M点时速度为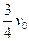
，再到P点与b球相碰并粘合在一起（碰撞时间极短），运动到N点时速度恰好为零。求：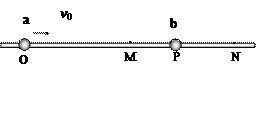
⑴电场强度E的大小和方向；
⑵a、b两球碰撞中损失的机械能；
⑶a球碰撞b球前的速度v。