厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数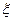 的分布列及期望
的分布列及期望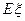 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
若方程x2-2ax+a=0在(0,1)恰有一个解,求a的取值范围.
已知函数 ,数列
,数列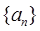 满足
满足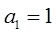 ,
, .
.
(1)求数列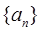 的通项公式;
的通项公式;
(2)令 ,求
,求 ;
;
(3)令 ,
, ,
,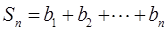 ,若
,若 对一切
对一切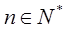 成立,求最小正整数
成立,求最小正整数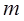 .
.
已知函数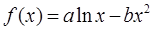 图象上一点
图象上一点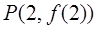 处
处
的切线方程为y= -3x+2ln2+2.
(1)求a,b的值;
(2)若方程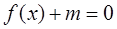 在
在 内有两个不等实根,求m的取值范围(其
内有两个不等实根,求m的取值范围(其
中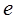 为自然对数的底数);
为自然对数的底数);
已知一动圆P(圆心为P)经过定点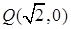 ,并且与定圆
,并且与定圆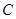 :
: (圆心为C)相切.
(圆心为C)相切.
(1)求动圆圆心P的轨迹方程;
(2)若斜率为k的直线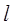 经过圆
经过圆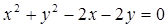 的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得
的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得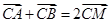 ?如果存在,求出
?如果存在,求出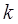 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
如图,在直三棱柱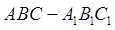 中,
中,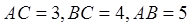 ,
,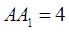 ,点D是AB的中点.
,点D是AB的中点.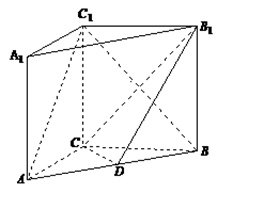
(1)求证: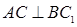 ;
;
(2)求证: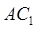 ∥平面
∥平面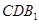 ;
;
(3)求异面直线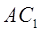 与
与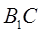 所成角的余弦值.
所成角的余弦值.