从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
.
(1)求从该批产品中任取1件是二等品的概率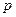 ;
;
(2)若该批产品共100件,从中任意抽取2件,求事件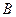 :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率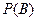 .
.
(本小题满分10分)经过点 ,倾斜角为
,倾斜角为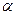 的直线
的直线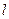 ,与曲线
,与曲线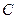 :
: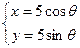 (
( 为参数)相交于
为参数)相交于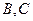 两点.
两点.
(1)写出直线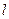 的参数方程,并求当
的参数方程,并求当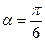 时弦
时弦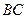 的长;[
的长;[
(2)当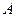 恰为
恰为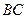 的中点时,求直线
的中点时,求直线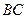 的方程;
的方程;
(3)当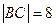 时,求直线
时,求直线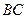 的方程;
的方程;
(4)当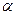 变化时,求弦
变化时,求弦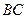 的中点的轨迹方程.
的中点的轨迹方程.
(本小题满分10分)设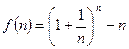 ,其中
,其中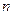 为正整数.
为正整数.
(1)求 ,
, ,
,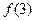 的值;
的值;
(2)猜想满足不等式 的正整数
的正整数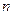 的范围,并用数学归纳法证明你的猜想.
的范围,并用数学归纳法证明你的猜想.
(本小题满分8分)设函数

 .
.
(1)当 时,解关于
时,解关于 的不等式
的不等式 ;
;
(2)如果 ,
, ,求
,求 的取值范围.
的取值范围.
已知各项均为正数的数列 的前 项和满足 ,且 .
(1)求
的通项公式;
(2)设数列
满足
,并记
为
的前
项和,求证:
.
已知函数
在
处取得极值
,其中
为常数。
(1)试确定
的值;
(2)讨论函数
的单调区间;
(3)若对任意
,不等式
恒成立,求
的取值范围.