(本小题12分)
(改编题)(理)
四个纪念币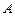 、
、 、
、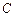 、
、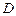 ,投掷时正面向上的概率如下表所示
,投掷时正面向上的概率如下表所示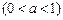 .
.
| 纪念币 |
A |
B |
C |
D |
| 概率 |
 |
 |
a |
a |
这四个纪念币同时投掷一次,设 表示出现正面向上的个数.
表示出现正面向上的个数.
(Ⅰ)求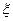 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)在概率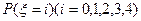 中,若
中,若 的值最大,求
的值最大,求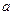 的取值范围;
的取值范围;
( 本小题12分) 某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案.抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(I)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人答:我只知道,从盒中抽取两张都是“世博会会徽”卡的概率是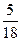 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(Ⅱ)在(I)下,甲乙丙丁四人依次抽奖,至少有两人获奖的概率.
(本小题13分)已知函数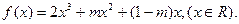
(1)当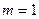 时,解不等式
时,解不等式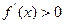 ;
;
(2)若曲线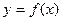 的所有切线中,切线斜率的最小值为
的所有切线中,切线斜率的最小值为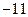 ,求
,求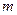 的值.
的值.
(本小题13分)已知集合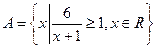 ,
,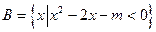 .
.
(1)当 时,求
时,求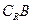 ;
;
(2)若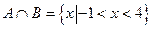 ,求实数
,求实数 的值.
的值.
(本小题13分)7名师生站成一排照相留念,其中老师1人,男生4人,女生2人,在下列情况下,各有不同站法多少种?(用数字作答)
(1)两名女生必须相邻而站;
(2)4名男生互不相邻.
(12分)设 。
。
(1)设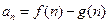 ,求
,求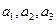 ,并证明
,并证明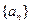 为递减数列;
为递减数列;
(2)是否存在常数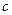 ,使
,使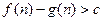 对
对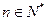 恒成立?若存在,试找出
恒成立?若存在,试找出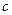 的一个值,并证明;若不存在,说明理由。
的一个值,并证明;若不存在,说明理由。