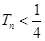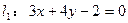
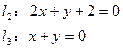
求证: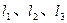 交于一点。
交于一点。
(本小题满分12分)某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
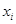 (月) (月) |
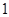 |
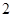 |
 |
 |
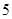 |
 (千克) (千克) |
 |
 |
 |
 |
 |
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图. 
(2)请根据上表提供的数据,用最小二乘法求出变量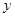 关于变量
关于变量 的线性回归直线方程
的线性回归直线方程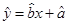 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: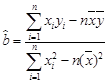 ,
, )
)
(本题12分)
设向量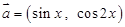 ,
,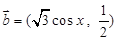 ,函数
,函数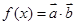
(1)求函数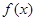 的最小正周期。
的最小正周期。
(2)若 ,
,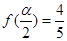 ,求
,求 的值
的值
(本小题满分14分)已知函数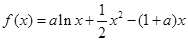 .
.
(1) 求函数 的单调区间;
的单调区间;
(2) 证明: 时,
时,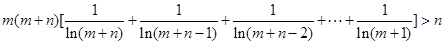 .
.
(本小题满分14分)已知抛物线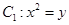 ,圆
,圆 .
.
(1)在抛物线 上取点
上取点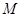 ,
,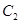 的圆周上取一点
的圆周上取一点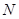 ,求
,求 的最小值;
的最小值;
(2)设
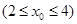 为抛物线
为抛物线 上的动点,过
上的动点,过 作圆
作圆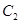 的两条切线,交抛物线
的两条切线,交抛物线 于
于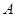 、
、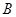 点,求
点,求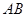 中点
中点 的横坐标的取值范围.
的横坐标的取值范围.
(本小题满分14分)已知数列 的前
的前 项和为
项和为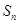 ,且
,且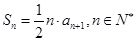 ,其中
,其中
(1)求数列 的通项公式;
的通项公式;
(2)若 ,数列
,数列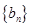 的前
的前 项和为
项和为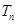 ,求证:
,求证: