已知A、B、C是△ABC的内角,向量 且
且 。
。
(1)求角A的大小;(2)若 ,求tanC 。
,求tanC 。
已知
(1)当a=1时,求 的单调区间
的单调区间

(2)是否存在实数a,使 的极大值为3?若存在,求出a的值,若不存在,说明理由.
的极大值为3?若存在,求出a的值,若不存在,说明理由.
|
已知函数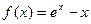 (
(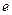 为自然对数的底数)
为自然对数的底数)

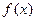 的最小值
的最小值
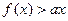 的解集为P,且
的解集为P,且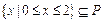 ,求实数a的取值范围
,求实数a的取值范围
已知函数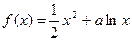 (a∈R).(1)若
(a∈R).(1)若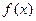 在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明:
在[1,e]上是增函数,求a的取值范围(2)若a=1,a≤x≤e,证明: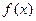 <
<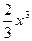
已知函数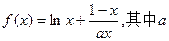 为大于零的常数。
为大于零的常数。

(1)若函数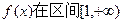 内单调递增,求a的取值范围
内单调递增,求a的取值范围
(2)求函数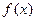 在区间[1,2]上的最小值。
在区间[1,2]上的最小值。
已知函数f(x)= x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R).
(1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.