如图所示，在光滑水平面的右端A处有一固定挡板P，挡板上固定一个轻质弹簧，在左测距挡板足够远处的B点竖直固定一半径为R的半圆形光滑轨道，在半圆轨道的顶端C处安装有压力传感器，用以记录到达此处的物体对轨道顶端的压力大小。将一质量为m的小球，放置在弹簧左侧并用力向右压弹簧，由静止释放，小球到达C点时，由压力传感器感知并通过计算机瞬间记录小球对C点的压力大小F，之后小球离开C点做平抛运动，落点与B点间的水平距离为x，改变最初弹簧的压缩量，并仍由静止释放小球，从而得到不同的F与x的值，如图所示为这一过程中F—x2图线，由此请回答：(g=10m/s2)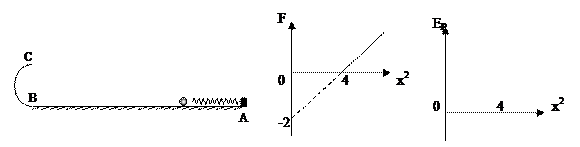
（１）求小球的质量与圆弧轨道的半径。
（２）由题意，并根据实际情况作出弹簧的弹性势能与x2的关系图线，并通过计算标出图线与直线x2=0和x2=4的交点的EP值。
如图所示，把一个质量m="1" kg的物体通过两根等长的细绳与竖直杆上A、B两个固定点相连接，绳a、b长都是1 m。AB长度是1.6 m，直杆和球旋转的角速度等于多少时，b绳上才有张力？
如图所示，水平台面AB距地面的高度h＝0.8m。有一滑块从A点以
＝6m/s的初速度在台面上做匀变速直线运动，滑块与平台间的动摩擦因数
=0.25。滑块运动到平台边缘的B点后水平飞出。己知AB＝2.2m。不计空气阻力，g取10
。求
（1）滑块从B点飞出时的速度大小；
（2）滑块落地点到平台边缘的水平距离。
在同一平台上的O点抛出的3个物体，做平抛运动的轨迹均在纸面内，如图所示，则3个物体做平抛运动的初速度
的关系及落地时间
的关系分别是（）
A． |
B． |
C． |
D． |
质量为m的飞机以水平速度
飞离跑道后逐渐上升，若飞机在此过程中水平速度保持不变，同时受到重力和竖直向上的恒定升力（该升力由其它力的合力提供，不含重力）。今测得当飞机在水平方向的位移为l时，它的上升高度为h。求：
（1）飞机受到的升力大小；
（2）从起飞到上升至h高度的过程中升力所做的功及在高度h处飞机的动能。
2008年5月12日，在四川省汶川县发生了8.0级大地震，造成了重大的人员伤亡和财产损失。灾难发生后，党和政府紧急采取各项救援工作。若一架执行救灾任务的飞机沿水平方向匀速飞行，相隔0.5s先后释放完全相同的两箱救灾物资1和2。在这两箱物资刚开始下落的一小段时间内，可以认为它们在水平方向上受到的空气阻力大小恒定，则在这一小段时间内，地上的人将看到（）
| A．1号箱在2号箱的正下方 | B．两箱间的水平距离保持不变 |
| C．两箱间的水平距离越来越大 | D．两箱间的水平距离越来越小 |