风能将成为21世纪大规模开发的一种可再生清洁能源。风力发电机是将风能(气流的功能)转化为电能的装置,其主要部件包括风轮机、齿轮箱,发电机等。如图所示。

(1)利用总电阻的线路向外输送风力发电机产生的电能。输送功率=300,输电电压=10,求导线上损失的功率与输送功率的比值;
(2)风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积。设空气密度为,气流速度为,风轮机叶片长度为。求单位时间内流向风轮机的最大风能;
在风速和叶片数确定的情况下,要提高风轮机单位时间接受的风能,简述可采取的措施。
(3)已知风力发电机的输出电功率与成正比。某风力发电机的风速时能够输出电功率。我国某地区风速不低于的时间每年约为5000小时,试估算这台风力发电机在该地区的最小年发电量是多少千瓦时。
用半径相同的两小球A、B的碰撞验证动量守恒定律.实验装置如图1625,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若测得各落点痕迹到O点的距离:OM="2.68" cm,OP="8.62" cm,ON="11.50" cm,并知A、B两球的质量比为2∶1,则未放B球时A球落地点是记录纸上的点,系统碰撞前,总动量p与碰撞后总动量p′的百分误差|p-p′|p=(结果保留一位有效数字).
大、小两个钢球在光滑的水平面上相撞,大球的质量是小球质量的4倍,当大球以某一速度与静止的小球碰撞后,大球沿原方向运动,速度大小为1.5 m/s,小球的速度为2 m/s,求开始时大球以多大的速度运动?
(1)如图6-15,在光滑水平长直轨道上,放着一个静止的弹簧振子,它由一轻弹簧两端各连接一个小球构成,两小球质量相等.现突然给左端小球一个向右的速度u0,求弹簧第一次恢复到自然长度时,每个小球的速度.
(2)如图6-16,将N个这样的振子放在该轨道上,最左边的振子1被压缩至弹簧为某一长度后锁定,静止在适当位置上,这时它的弹性势能为E0.其余各振子间都有一定的距离,现解除对振子1的锁定,任其自由运动,当它第一次恢复到自然长度时,刚好与振子2碰撞,此后,继续发生一系列碰撞,每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰.求所有可能的碰撞都发生后,每个振子弹性势能的最大值.已知本题中两球发生碰撞时,速度交换,即一球碰后的速度等于另一球碰前的速度.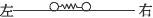
图6-15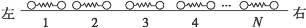
图6-16
如图6-12质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩,现在挂钩上挂一质量为m3的物体C并从静止状态释放,已知它恰好能使B离开地面但不继续上升.若将C换成另一个质量为(m1+m3)的物体D,仍从上述初始位置由静止状态释放,则这次B刚离地时D的速度的大小是多少?已知重力加速度为g.
图6-12
在原子核物理中,研究核子与核子关联的最有效途径是“双电荷交换反应”.这类反应的前半部分过程和下述力学模型类似.两个小球A和B用轻质弹簧相连,在光滑的水平轨道上处于静止状态.在它们左边有一垂直于轨道的固定挡板P,右边有一个小球C沿轨道以速度v0射向B球,如图6-4-9所示,C与B发生碰撞并立即结成一个整体D.在它们继续向左运动的过程中,当弹簧长度变到最短时,长度突然被锁定,不再改变.然后,A球与挡板P发生碰撞,碰后A、D都静止不动,A与P接触而不黏连.过一段时间,突然解除锁定(锁定及解除锁定均无机械能损失).已知A、B、C三球的质量均为m,求: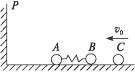
图6-4-9
(1)弹簧长度刚被锁定后A球的速度;
(2)在A球离开挡板P之后的运动过程中,弹簧的最大弹性势能.