如图所示,质量为2kg的物块A(可看作质点),开始放在长木板B的左端,B的质量为1kg,可在水平面上无摩擦滑动,两端各有一竖直挡板MN,现A、B以相同的速度v0=6m/s向左运动并与挡板M发生碰撞.B与M碰后速度立即变为零,但不与M粘接;A与M碰撞没有能量损失,碰后接着返向N板运动,且在与N板碰撞之前,A、B均能达到共同速度并且立即被锁定,与N板碰撞后A、B一并原速反向,并且立刻解除锁定.A、B之间的动摩擦因数μ=0.1.通过计算回答下列问题:
(1)A与挡板M能否发生第二次碰撞?
(2)A和最终停在何处?
(3)A在B上一共通过了多少路程?
如图所示,可视为质点的三物块A、B、C放在倾角为300、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=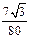 ,A与B紧靠在一起,C紧靠在固定挡板上,三物块的质量分别为mA=0.80kg、mB=0.64kg、mC=0.50kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5C、qC=+2.0×10-5C且保持不变,开始时三个物块均能保持静止且与斜面间均无摩擦力作用。如果选定两点电荷在相距无穷远处的电势能为零,则相距为r时,两点电荷具有的电势能可表示为
,A与B紧靠在一起,C紧靠在固定挡板上,三物块的质量分别为mA=0.80kg、mB=0.64kg、mC=0.50kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5C、qC=+2.0×10-5C且保持不变,开始时三个物块均能保持静止且与斜面间均无摩擦力作用。如果选定两点电荷在相距无穷远处的电势能为零,则相距为r时,两点电荷具有的电势能可表示为 。现给A施加一平行于斜面向上的力F,使A在斜面上一直作加速度a=1.5m/s2的匀加速直线运动,经过时间t0,力F变为恒力,当A运动到斜面顶端时撤去力F。已知静电力常量k=9.0×109N·m2/C2,g=10m/s2。求:
。现给A施加一平行于斜面向上的力F,使A在斜面上一直作加速度a=1.5m/s2的匀加速直线运动,经过时间t0,力F变为恒力,当A运动到斜面顶端时撤去力F。已知静电力常量k=9.0×109N·m2/C2,g=10m/s2。求: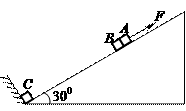
(1)未施加力F时物块B、C间的距离;
(2)t0时间内A上滑的距离;
(3)力F对A物块做的总功。
如图(a),质量m的物体沿倾角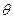 的固定粗糙斜面由静止开始向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k表示,物体加速度a与风速v的关系如图(b)所示。求:
的固定粗糙斜面由静止开始向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k表示,物体加速度a与风速v的关系如图(b)所示。求: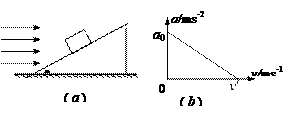
(1)物体与斜面间的动摩擦因数m;
(2)比例系数k。
一质量为M的汽艇,在静水中航行时能达到的最大速度为10m/s。假设航行时,汽艇的牵引力F始终恒定不变,而且汽艇受到的阻力f与其航速v之间,始终满足关系:f=kv,其中k=100N·s/m,不计水的粘性,各速度均为对地值。求:
⑴该汽艇的速度达到5m/s的瞬时,汽艇受到的阻力为多大?
⑵该汽艇的牵引力F为多大?
⑶若水被螺旋桨向后推出的速度为8m/s,汽艇以最大速度匀速行驶时,在3秒钟之内,估算螺旋桨向后推出水的质量m为多少?
如图,光滑的U型金属导轨PQMN水平地固定在竖直向上的匀强磁场中.磁感应强度为B,导轨的宽度为L,其长度足够长,QM之间接有一个阻值为R的电阻,其余部分电阻不计。一质量为m,电阻也为R的金属棒ab,恰能放在导轨之上并与导轨接触良好。当给棒施加一个水平向右的冲量,棒就沿轨道以初速度v0开始向右滑行。求: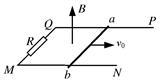
⑴开始运动时,棒中的瞬间电流i和棒两端的瞬间电压u分别为多大?
⑵当棒的速度由v0减小到v0/10的过程中,棒中产生的焦耳热Q是多少?棒向右滑行的位移x有多大?
真空环境中存在竖直向上的匀强电场和匀强磁场,电场强度E=10.0V/m,磁感应强度B=3.14T.现在此空间建立xyz三维坐标系,其中x轴水平向右、y轴水平向里、z轴竖直向上,三坐标轴的单位均为米(m),一带电油滴恰好悬停在坐标原点。t1=0时刻油滴受瞬间的水平冲量(油滴质量、电量不变),以 =3.14m/s的速度沿x轴正方向运动;t2=1.50s时刻撤去匀强磁场;t3=2.50s时刻撤去匀强电场。取g=10m/s2,试求t4=3.00s时刻油滴所在位置的坐标(计算结果取三位有效数字)。
=3.14m/s的速度沿x轴正方向运动;t2=1.50s时刻撤去匀强磁场;t3=2.50s时刻撤去匀强电场。取g=10m/s2,试求t4=3.00s时刻油滴所在位置的坐标(计算结果取三位有效数字)。