如图演示用的手摇发电机模型，匀强磁场磁感应强度Ｂ＝０，5T,线圈匝数N=50匝,每匝线圈面积为0，48m
,转速为150r/min。在匀速转动过程中,从图示位置线圈转过90°开始计时。
⑴写出交流感应电动势瞬时值的表达式。
⑵画出e-t图线。
.如图所示，平行且足够长的两条光滑金属导轨，相距0.5m，与水平面夹角为30°，不计电阻，广阔的匀强磁场垂直穿过导轨平面，磁感应强度B＝0.4T，垂直导轨放置两金属棒ab和cd，长度均为0.5m，电阻均为0.1Ω，质量分别为0.1 kg和0.2 kg，两金属棒与金属导轨接触良好且可沿导轨自由滑动．现ab棒在外力作用下，以恒定速度v＝1.5m／s沿着导轨向上滑动，cd棒则由静止释放，试求： (取g＝10m／s2)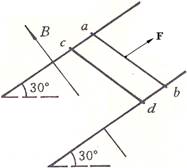
（1）金属棒ab产生的感应电动势；
（2）闭合回路中的最小电流和最大电流；
（3）金属棒cd的最终速度．
.如图所示，质量为m的跨接杆ab可以无摩擦地沿水平的导轨滑行，两轨间距为L，导轨一端与电阻R连接，放在竖直向下的匀强磁场中，磁感应强度为B。杆从x轴原点O以大小为v0的水平初速度向右滑行，直到停下。已知杆在整个运动过程中速度v和位移x的函数关系是：v＝v0－。杆与导轨的电阻不计。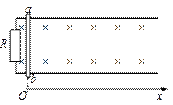
（1）试求杆所受的安培力F随其位移x变化的函数式；
（2）分别求出杆开始运动和停止运动时所受的安培力F1和F2；
（3）证明杆在整个运动过程中动能的增量DEk等于安培力所做的功W；
（4）求出电阻R所增加的内能DE。
一位身高1.80 m的跳高运动员擅长背越式跳高，他经过25 m弧线助跑，下蹲0.2 m蹬腿、起跳，划出一道完美的弧线，创造出他的个人最好成绩2.39 m（设其重心C上升的最大高度实际低于横杆0.1 m）。如果他在月球上采用同样的方式起跳和越过横杆，请估算他能够跃过横杆的高度为多少？
某同学认为：该运动员在地球表面能够越过的高度H＝＋0.1，则有v0＝¼
该名运动员在月球上也以v0起跳，能够越过的高度H’＝＋0.1¼
根据万有引力定律，月球表面的重力加速度为地球表面重力加速度的1/6，所以H’＝¼
你觉得这位同学的解答是否合理？如果是，请完成计算；如果你觉得不够全面，请说明理由，并请用你自己的方法计算出相应的结果。
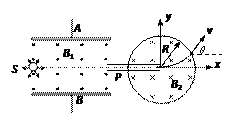
如图所示为一离子选择器。极板A、B间距为d，用来研究粒子的种类及偏向角。在A、B间加电压，B板电势高于A板电势，且A、B极板间有垂直纸面向外的匀强磁场，磁感应强度为B1。P为一内壁光滑、缘绝两端开口的直细管，右端的开口在半径为R的圆形磁场区域中心O点（作为坐标原点），此磁场方向垂直纸面向里，磁感应强度为B2（细管中不存在磁场）。细管的中心轴所在的直线通过S粒子源，粒子源可发出电荷量为q、质量为m、速度大小和方向都不同的粒子，当有粒子从圆形磁场区域射出时，其速度方向与x轴的夹角为偏向角。不计粒子重力。⑴若已知A、B间电压值为U，求从磁场B1射出能射入P管的粒子速度v的大小；⑵若粒子能从圆形区域磁场B2射出，其偏向角为θ，求A、B间的电压值U；⑶粒子能从圆形区域磁场B2射出时，A、B间的电压值应满足什么条件？
 |
1
如图7所示，水平的平行虚线间距为d=50cm，其间有B=1.0T的匀强磁场。一个正方形线圈边长为l=10cm，线圈质量m=100g，电阻为R=0.020Ω。开始时，线圈的下边缘到磁场上边缘的距离为h=80cm。将线圈由静止释放，其下边缘刚进入磁场和刚穿出磁场时的速度相等。取g=10m/s2，求：⑴线圈进入磁场过程中产生的电热Q。⑵线圈下边缘穿越磁场过程中的最小速度v。⑶线圈下边缘穿越磁场过程中加速度的最小值a。