如图所示,质量mA为4.0kg的木板A放在水平面C上,木板与水平面间的动摩擦因数μ为0.24,木板右端放着质量mB为1.0kg的小物块B(视为质点),它们均处于静止状态.木板突然受到水平向右的12N·s的瞬时冲量作用开始运动,当小物块滑离木板时,木板的动能EKA为8.0J,小物块的动能EKB为0.50J,重力加速度取10m/s2,求:
(1)瞬时冲量作用结束时木板的速度υ0;
(2)木板的长度L.
如图,位于水平面上的质量为M的小木块,在大小为F,方向与水平方向为α角的拉力作用用下沿着地面作匀速直线运动,求
(1)地面对物体的支持力
(2)木块与地面之间的动摩擦因数?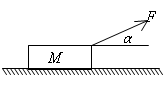
用绳子AO和BO吊起一个重100N的物体,两绳AO,BO与竖直方向的夹角为30度和45度,求绳子AO,BO对物体的拉力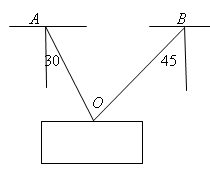
在一次测试中,质量为1.6×103kg的汽车沿平直公路行驶,其发动机的输出功率恒为100kW。汽车的速度由10m/s增加到16m/s,用时1.7s,行驶距离22.6m。若在这个过程中汽车所受的阻力恒定,则汽车的速度为10m/s时牵引力的大小为 N,此时汽车加速度的大小为 m/s2。
火车在平直公路上作匀加速直线运动,车头通过某路标时,速度v1,车尾通过路标时的速度v2,则车的中点通过该路标的速度为?
如图2-2所示水平放置的粗糙的长木板上放置一个物体m,当用于缓慢抬起一端时,木板受到的压力和摩擦力将怎样变化?