已知函数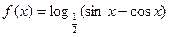 (1)求f(x)的定义域;(2)判断f(x)的奇偶性。
(1)求f(x)的定义域;(2)判断f(x)的奇偶性。
如图所示的几何体ABCDFE中,△ABC,△DFE都是等边三角形,且所在平面平行,四边形BCED为正方形,且所在平面垂直于平面ABC.
(Ⅰ)证明:平面ADE∥平面BCF;
(Ⅱ)求二面角D-AE-F的正切值.
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
已知函数f(x)=cos(2x- )+sin2x-cos2x.
)+sin2x-cos2x.
(Ⅰ)求函数f(x)的最小正周期及其图象的对称轴方程;
(Ⅱ)设函数g(x)=[f(x)]2+f(x),求g(x)的值域.
已知函数 .
.
(Ⅰ)请写出函数 在每段区间上的解析式,并在图中的直角坐标系中作出函数
在每段区间上的解析式,并在图中的直角坐标系中作出函数 的图象;
的图象;
(II)若不等式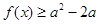 对任意的实数
对任意的实数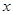 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知在直角坐标系 中,曲线
中,曲线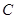 的参数方程为:
的参数方程为: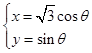 (
(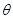 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点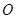 为极点,以
为极点,以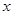 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线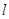 的极坐标方程为:
的极坐标方程为: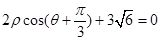 .
.
(Ⅰ)写出曲线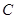 和直线
和直线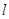 在直角坐标系下的方程;
在直角坐标系下的方程;
(II)设点 是曲线
是曲线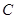 上的一个动点,求它到直线
上的一个动点,求它到直线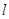 的距离的最小值.
的距离的最小值.