数列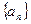 满足
满足 ,
,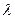 是常数.
是常数.
⑴当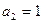 时,求
时,求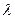 及
及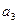 的值;
的值;
⑵数列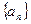 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
⑶求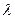 的取值范围,使得存在正整数
的取值范围,使得存在正整数 ,当
,当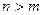 时总有
时总有 .
.
如图,椭圆
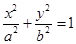 (
(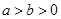 )经过点
)经过点 ,且离心率为
,且离心率为 .
.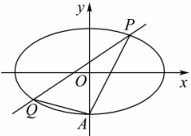
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)经过点 ,且斜率为
,且斜率为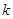 的直线与椭圆
的直线与椭圆 交于不同两点
交于不同两点 ,
, (均异于点
(均异于点 ),证明:直线
),证明:直线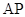 与
与 的斜率之和为
的斜率之和为 .
.
在等差数列 中,
中,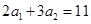 ,
,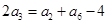 ,其前
,其前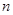 项和为
项和为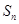 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 满足
满足 ,求数列
,求数列 的前
的前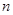 项和
项和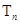 .
.
已知四棱锥 ,其中
,其中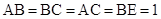 ,
, ,
,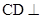 面
面 ,
,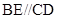 ,
, 为
为 的中点.
的中点.
(Ⅰ)求证: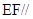 面
面 ;
;
(Ⅱ)求证:面 面
面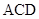 ;
;
(III)求四棱锥 的体积.
的体积.
 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .向量
.向量 与
与 平行.
平行.
(Ⅰ)求角 ;
;
(Ⅱ)若 ,
, ,求
,求 的面积.
的面积.
某个团购网站为了更好地满足消费者,对在其网站发布的团购产品展开了用户调查,每个用户在使用了团购产品后可以对该产品进行打分,最高分是 分.上个月该网站共卖出了
分.上个月该网站共卖出了 份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组
份团购产品,所有用户打分的平均分作为该产品的参考分值,将这些产品按照得分分成以下几组:第一组 ,第二组
,第二组 ,第三组
,第三组 ,第四组
,第四组 ,第五组
,第五组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(Ⅰ)分别求第三,四,五组的频率;
(Ⅱ)该网站在得分较高的第三,四,五组中用分层抽样的方法抽取了 个产品作为下个月团购的特惠产品,某人决定在这
个产品作为下个月团购的特惠产品,某人决定在这 个产品中随机抽取
个产品中随机抽取 个购买,求他抽到的两个产品均来自第三组的概率.
个购买,求他抽到的两个产品均来自第三组的概率.