已知函数f(x)=,数列{xn}的通项由xn=f(xn-1)(n≥2,且n∈N*)确定.
(1)求证:{}是等差数列;
(2)当x1=时,求x100.
(本题满分12)
已知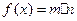 ,其中
,其中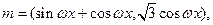
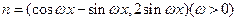 .若
.若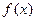 图象中相邻的对称轴间的距离不小于
图象中相邻的对称轴间的距离不小于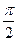 .
.
(1)求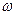 的取值范围
的取值范围
(2)在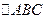 中,
中,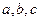 分别为角
分别为角 的对边.且
的对边.且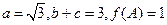 ,当
,当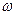 最大时.求
最大时.求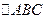 面积.
面积.
(4-5不等式选讲)(本小题10分)
设函数 .
.
⑴求不等式 的解集;
的解集;
⑵求函数 的最小值.
的最小值.
(4-4极坐标与参数方程)(本小题10分)
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数).
(θ为参数).
⑴将曲线C的参数方程化为普通方程;
⑵若直线l与曲线C交于A、B两点,求线段AB的长.
(4-1几何证明选讲)(本小题10分)
如图圆O和圆 相交于A,B两点,AC是圆
相交于A,B两点,AC是圆 的切线,AD
的切线,AD 是圆O的切线,若BC=2,AB=4,求BD.
是圆O的切线,若BC=2,AB=4,求BD.
(本小题满分12分)
已知 、B、C是椭圆M:
、B、C是椭圆M: 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为 ,BC过椭圆M的中心,且
,BC过椭圆M的中心,且
(1)求椭圆M的方程;
(2)过点 的直线
的直线 (斜率存在时)与椭圆M交于两点P、Q,设D为椭圆M与
(斜率存在时)与椭圆M交于两点P、Q,设D为椭圆M与 轴负半轴的交点,且
轴负半轴的交点,且 求实数
求实数 的取值范围.
的取值范围.