(4-4极坐标与参数方程)(本小题10分)
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数).
(θ为参数).
⑴将曲线C的参数方程化为普通方程;
⑵若直线l与曲线C交于A、B两点,求线段AB的长.
已知函数f(x)=2x+k·2-x,k∈R.
(1)若函数f(x)为奇函数,求实数k的值;
(2)若对任意的x∈[0,+∞)都有f(x)>2-x成立,求实数k的取值范围.
已知集合A={y|y2-(a2+a+1)y+a(a2+1)>0},B={y|y= x2-x+
x2-x+ ,0≤x≤3}.
,0≤x≤3}.
(1)若A∩B=∅,求a的取值范围;
(2)当a取使不等式x2+1≥ax恒成立的a的最小值时,求(∁RA)∩B.
某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行次数n |
输出y的值 为1的频数 |
输出y的值 为2的频数 |
输出y的值 为3的频数 |
| 30 |
14 |
6 |
10 |
| … |
… |
… |
… |
| 2 100 |
1 027 |
376 |
697 |
乙的频数统计表(部分)
| 运行次数n |
输出y的值 为1的频数 |
输出y的值 为2的频数 |
输出y的值 为3的频数 |
| 30 |
12 |
11 |
7 |
| … |
… |
… |
… |
| 2 100 |
1 051 |
696 |
353 |
当n=2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;
(3)将按程序框图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
| 品牌 |
甲 |
乙 |
|||
| 首次出现故障时间x(年) |
0<x≤1 |
1<x≤2 |
x>2 |
0<x≤2 |
x>2 |
| 轿车数量(辆) |
2 |
3 |
45 |
5 |
45 |
| 每辆利润(万元) |
1 |
2 |
3 |
1.8 |
2.9 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率;
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列;
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
如图所示,已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=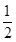 ,斜率为2的直线l过点A(2,3).
,斜率为2的直线l过点A(2,3).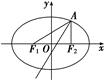
(1)求椭圆E的方程;
(2)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.