过点 的椭圆 的离心率为 ,椭圆与 轴交于两点 、 ,过点 的直线 与椭圆交于另一点 ,并与 轴交于点 ,直线 与直线 交于点 .
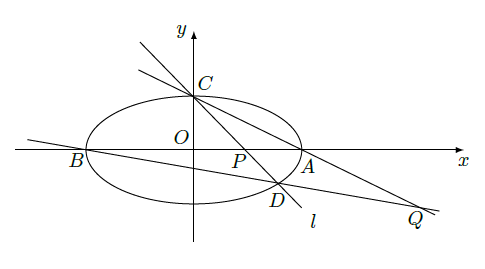
(I)当直线
过椭圆右焦点时,求线段
的长;
(Ⅱ)当点
异于点
时,求证:
如图所示,已知半圆的直径AB=2,点C在AB 的延长线上,BC=1,点P为半圆上的一个动点,以
的延长线上,BC=1,点P为半圆上的一个动点,以
DC为边作等边△PCD,且点D与圆心O分别在PC
的两侧,求四边形OPDC面积的最大值.
沿一条小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是
50°,距离是3 km,从B到C,方位角是110°,距离是3 km,从C到D,方位角是140°,距离是(9+3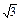 )km.试画出示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出示意图,并计算出从A到D的方位角和距离(结果保留根号).
在△ABC中,角A、B、C的对边分别为a、b、c,已知a+b=5,c= ,且4sin2
,且4sin2 -cos2C=
-cos2C= .
.
(1)求角C的大小;
(2)求△ABC的面积.
已知a、b、c是△ABC的三边长,关于x的方程ax2-2 x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10
x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10 ,c=7.
,c=7.
(1)求角C;
(2)求a,b的值.
在△ABC中,cosB=- ,cosC=
,cosC= .
.
(1)求sinA的值;
(2)△ABC的面积S△ABC= ,求BC的长.
,求BC的长.