如图22所示，两个共轴的圆筒形金属电极，外电极接地，其上均匀分布着平行于轴线的四条狭缝ａ、ｂ、ｃ和ｄ，外筒的外半径为ｒ，在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场，磁感强度的大小为Ｂ。在两极间加上电压，使两圆筒之间的区域内有沿半径向外的电场。一质量为ｍ、带电量为＋ｑ的粒子，从紧靠内筒且正对狭缝ａ的Ｓ点出发，初速为零。如果该粒子经过一段时间的运动之后恰好又回到出发点Ｓ，则两电极之间的电压Ｕ应是多少？（不计重力，整个装置在真空中）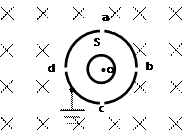
如图所示，一个质量为m、带电量为＋q的小球，以初速度v0自h高度处水平抛出。不计空气阻力。重力加速度为g。
（1）若在空间竖直方向加一个匀强电场，发现小球水平抛出后做匀速直线运动，求该匀强电场的场强E的大小；
（2）若在空间再加一个垂直纸面向外的匀强磁场，小球水平抛出后恰沿圆弧轨迹运动，落地点P到抛出点的距离为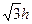
，求该磁场磁感应强度B的大小。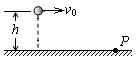
如图所示，有一区域足够大的匀强磁场，磁感应强度为B，磁场方向与水平放置的导轨垂直。导轨宽度为L，右端接有电阻R。MN是一根质量为m的金属棒，金属棒与导轨垂直放置，且接触良好，金属棒与导轨电阻均不计。金属棒与导轨间的动摩擦因数为μ，现给金属棒一水平初速度v0，使它沿导轨向左运动。已知金属棒停止运动时位移为s。求：
（1）金属棒速度为v时的加速度为多大？
（2）金属棒运动过程中通过电阻R的电量q；
（3）金属棒运动过程中回路产生的焦耳热Q。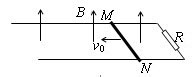
一架军用直升机悬停在距离地面64 m的高处，将一箱军用物资由静止开始投下，如果不打开物资上的自动减速伞，物资经4s落地。为了防止物资与地面的剧烈撞击，须在物资距离地面一定高度时将物资上携带的自动减速伞打开。已知物资接触地面的安全限速为2m/s，减速伞打开后物资所受空气阻力是打开前的18倍。减速伞打开前后空气阻力均认为大小不变，忽略减速伞打开的时间，取g="10" m/s2。求
（1）减速伞打开时离地面的高度至少为多少？
（2）物资运动的时间至少为多少？
如图所示，有一长为L的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好能在竖直面内做完整的圆周运动。已知水平地面上的C点位于O点正下方，且到O点的距离为1.9L。不计空气阻力。求：
（1）小球通过最高点A时的速度vA；
（2）小球通过最低点B时，细线对小球的拉力T；
（3）若小球运动到最低点B时细线恰好断裂，小球落地点到C点的距离。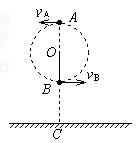
如图所示，粗细均匀一端封闭、一端开口的细玻璃管总长为100cm，中央折成直角，使它一半水平，一半竖直，外界大气压为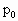
＝76cmHg不变，管内有30cm长的水银柱将一部分空气封闭于封闭端，当管内空气为－17℃时，空气柱长40cm．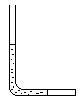
(1)当管内气体温度上升到30℃时，管内空气柱有多长？
(2)要将管内水银全部排空，管内气温至少应大于多少摄氏度？(假设温度上升是缓慢的)