(本小题满分12分)
已知函数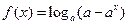
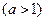 ,求
,求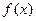 的定义域和值域;
的定义域和值域;
(本小题满分12分)
某地方政府为地方电子工业发展,决定对某一进口电子产品征收附加税。已知这种电子产品国内市场零售价为每件250元,每年可销售40万件,若政府征收附加税率为t元时,则每年减少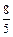 y万件。
y万件。
(1)收入表示为征收附加税率的函数;
(2)在 该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围?
该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围?
(本小题满分12分)求函数y= (4x-x2)的单调区间.
(4x-x2)的单调区间.
(本小题满分12分)
解方程:(1)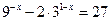 (2)
(2)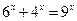
(本小题满分12分)
某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次减少 ,问过滤几次
,问过滤几次 才能使产品达到市场要求?
才能使产品达到市场要求?