已知双曲线E的离心率为e，左、右两焦点分别为F1、F2，抛物线C以F2为顶点，F1为焦点,点P为抛物线与双曲线右支上的一个交点，若a|PF2|＋c|PF1|＝8a2（其中a、c分别为双曲线的实半轴长和半焦距），则e的值为 ( )
| A． | B．3 | C． | D． |
已知函数f（x）是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足: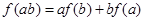 
, 
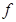（2）="2," an=
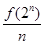（n∈N*）, bn=
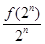（n∈N*）.
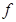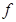考察下列结论: ①（0）= （1）;②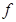（x）为偶函数; ③数列{an}为等比数列; ④数列{bn}为等差数列.其中正确的结论共有（）
| A．1个 | B．2个 | C．3个 | D．4个 |
已知函数f（x）=
，若a，b，c互不相等，且f（a）=f（b）=f（c），则a+b+c的取值范围为（）
A．（ ） |
B．（ ） |
C．（ ，12） |
D．（6，l2） |
已知一个空间几何体的三视图如图所示，其中俯视图是边长为6的正三角形，若这个空间几何体存在唯一的一个内切球（与该几何体各个面都相切），则这个几何体的全面积是（）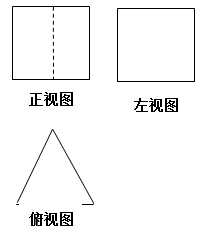
A．18 |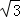
B．36 |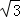
C．45 |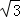
D．54 |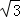
对于任意实数a，b，c，定义Г（a，b，c）满足Г（a，b，c）=Г（b，c，a）=Г（c，a，b）关系式，则称Г（a，b，c）具有轮换对称关系，给出如下四个式子：
①Г（a，b，c）=a+b+c；
②Г（a，b，c）=a2﹣b2+c2；
③Г（x，y，z）=xy+yz+zx；
④Г（A，B，C）=2sⅠnAsⅠnBsⅠnC+cos（
﹣A）sⅠn（π﹣B）sⅠnC（A、B、C是△ABC的内角）
其中具有轮换对称关系的个数是（）
A．1B．2 C．3 D．4
在正四面体P﹣ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的是（）
| A．BC∥平面PDF | B．DF⊥平面PAE |
| C．平面PDF⊥平面ABC | D．平面PAE⊥平面ABC |