已知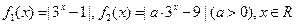 ,
,
且 .
.
(Ⅰ)当 时,求
时,求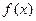 在
在 处的切线方程;
处的切线方程; (Ⅱ)当
(Ⅱ)当 时,设
时,设 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为 (闭区间
(闭区间 的长度定义为
的长度定义为 ),试求
),试求 的最大值;
的最大值;
如图,已知双曲线
的右焦点
,点
分别在
的两条渐近线上,
轴,
(
为坐标原点).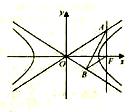
(1)求双曲线
的方程;
(2)过
上一点
的直线
与直线
相交于点
,与直线
相交于点
,证明点
在
上移动时,
恒为定值,并求此定值.
如图,四棱锥 中, 为矩形,平面 平面 .

(1)求证:
(2)若 问 为何值时,四棱锥 的体积最大?并求此时平面 与平面 夹角的余弦值.
已知函数
.
(1)当
时,求
的极值;
(2)若
在区间
上单调递增,求
的取值范围.
已知首项都是1的两个数列
(
),满足
.
(1)令
,求数列
的通项公式;
(2)若
,求数列
的前
项和
已知函数 ,其中
(1)当
时,求
在区间
上的最大值与最小值;
(2)若
,求
的值.