等差数列 中,
中, ,其公差
,其公差 ;数列
;数列 是等比数列,
是等比数列, ,其公比
,其公比
⑴若 ,试比较
,试比较 与
与 的大小,说明理由;
的大小,说明理由;
⑵若 ,试比较
,试比较 与
与 的大小,说明理由.
的大小,说明理由.
某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在的地区附近有A,B,C三家社区医院,并且他们对社区医院的选择是相互独立的.
(I)求甲、乙两人都选择A社区医院的概率;
(II)求甲、乙两人不选择同一家社区医院的概率;
(III)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
已知函数 .
.
(I)求函数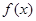 的最小正周期和值域;
的最小正周期和值域;
(II)若 为第二象限角,且
为第二象限角,且 ,求
,求 的值.
的值.
对于函数 ,若存在实数
,若存在实数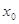 ,使
,使 成立,则称
成立,则称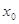 为
为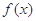 的不动点.
的不动点.
⑴当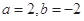 时,求
时,求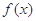 的不动点;
的不动点;
⑵若对于任何实数 ,函数
,函数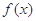 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数 的取值范围;
的取值范围;
⑶在⑵的条件下,若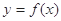 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数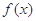 的不动点,且直线
的不动点,且直线 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
设集合A中不含有元素 ,且满足条件:若
,且满足条件:若 ,则有
,则有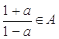 ,
,
请考虑以下问题:
(1)已知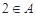 ,求出A中其它所有元素;
,求出A中其它所有元素;
(2)自己设计一个实数属于A,再求出A中其它所有元素;
(3)根据已知条件和前面(1)(2)你能悟出什么道理来,并证明你的猜想.
已知命题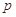 :方程
:方程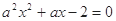 在[-1,1]上有解;命题
在[-1,1]上有解;命题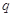 :只有一个实数
:只有一个实数 满足不等式
满足不等式 ,若命题“
,若命题“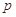 或
或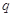 ”是假命题,求实数
”是假命题,求实数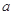 的取值范围.
的取值范围.