已知数列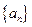 满足
满足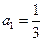 ,
,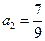 ,
,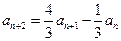
 .
.
⑴求数列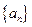 的通项公式;
的通项公式;
⑵求数列 的前
的前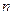 项和
项和 ;
;
(本小题满分13分)已知全集U=R, ,集合
,集合 .
.
(1)当 时,求
时,求 ;
;
(2)命题 :
: ,命题
,命题 :
: ,若
,若 是
是 的充分条件,求实数m的取值范围.
的充分条件,求实数m的取值范围.
(本小题满分14分)设函数 .
.
(1)若函数 在
在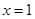 处与直线
处与直线 相切:
相切:
①求实数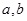 的值;
的值;
②求函数 在
在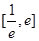 上的最大值;
上的最大值;
(2)当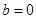 时,若不等式
时,若不等式 ≥
≥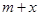 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)某渔业公司年初用98万元购得一艘捕渔船,第一年各种费用12万元,以后每年都增加4万元,每年的捕鱼收益50万元
(1)第几年开始获利?
(2)若干年后,有两种处理方案:
①年平均获利最大时,以26万元出售该渔船;
②总纯收入获利最大时,以8万元出售该渔船。请问:选择哪种方案更好?
(本小题满分13分) 已知函数f(x)= sin
sin  cos
cos +cos2
+cos2 .
.
(1)若f(x)=1,求cos 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足acos C+ c=b,求f(B)的取值范围.
c=b,求f(B)的取值范围.
(本小题满分13分)如图,四棱锥P—ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC= AD=1.
AD=1. 
(1)求证:面PAC⊥面PCD;
(2)在棱PD上是否存在一点E,使CE∥面PAB?若存在,请确定E点的位置;若不存在,请说明理由.