(本小题满分12分)
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为 ,
, ,
, ,
, ,由此得到样本的重量频率分布直方图(如下图),
,由此得到样本的重量频率分布直方图(如下图),
(1)求 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(2)从盒子中随机抽取 个小球,其中重量在
个小球,其中重量在 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).
(本小题满分12分)
已知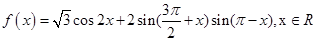
(1)求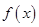 最小正周期及单调增区间;
最小正周期及单调增区间;
(2)已知锐角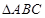 的内角
的内角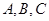 的对边分别为
的对边分别为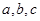 ,且
,且 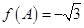 ,
,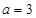 ,
,
求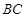 边上的高的最大值.
边上的高的最大值.
(本题满分10分)
若一个正实数能写成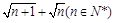 的形式,则称其为“兄弟数”.
的形式,则称其为“兄弟数”.
求证:(1)若 为“兄弟数”,则
为“兄弟数”,则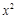 也为“兄弟数”;
也为“兄弟数”;
(2)若 为“兄弟数”,
为“兄弟数”,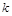 是给定的正奇数,则
是给定的正奇数,则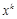 也为“兄弟数”.
也为“兄弟数”.
(本题满分10分)
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是: .
.
(1)求图中 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在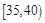 岁的人数;
岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动,再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人,记这3名志愿者中“年龄低于35岁”的人数为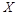 ,求
,求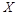 的分布列及数学期望.
的分布列及数学期望.
选修4—4:极坐标与参数方程
已知圆的极坐标方程为: .
.
(1)将极坐标方程化为普通方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.