一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数: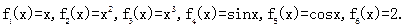 现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数
现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数 的分布列.
的分布列.
某校为了解高一年级学生身高情况,按10%的比例对全校700名高一学生按性别进行抽样检查,测得身高频数分布表如下:
表1:男生身高频数分布表
| 身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190) |
| 频数 |
2 |
5 |
13 |
13 |
5 |
2 |
表2:女生身高频数分布表
| 身高(cm) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
| 频数 |
1 |
8 |
12 |
5 |
3 |
1 |
(Ⅰ)求该校高一男生的人数;
(Ⅱ)估计该校高一学生身高(单位:cm)在[165,180)的概率;
(Ⅲ)在男生样本中,从身高(单位:cm)在[180,190)的男生中任选3人,设ξ表示所选3人中身高(单位:cm)在[180,185)的人数,求ξ的分布列和数学期望.
| ξ |
1 |
2 |
3 |
 |
 |
 |
 |
如图,四棱锥P-ABCD中,PD⊥底面ABCD,PD=DC=2AD,AD⊥DC,∠BCD=45°.
(Ⅰ)设PD的中点为M,求证:AM 平面PBC;
平面PBC;
(Ⅱ)求PA与平面PBC所成角的正切值.
已知数列{ }的前n项和
}的前n项和
(Ⅰ) 求数列{ }的通项公式;(Ⅱ) 设
}的通项公式;(Ⅱ) 设 ,求数列
,求数列 的前
的前 .
.
已知函数
 的图象如图所示.
的图象如图所示.
(1)求函数 的解析式;
的解析式;
(2)设 ,且方程
,且方程 有两个不同的实数根,求实数
有两个不同的实数根,求实数 的取值范围和这两个根的和;
的取值范围和这两个根的和;
(3)在锐角 中,若
中,若 ,求
,求 的取值范围.
的取值范围.
化简
(Ⅰ)
(Ⅱ)