某研究机构准备举办一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示
| 版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
| 人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,问这2人使用相同版本教材的概率是多少?
(2)若随机选出的2名教师都使用人教版教材,现设使用人教A版教材的教师人数为 ,求随机变量
,求随机变量 的分布列
的分布列
在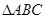 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是 ,已知
,已知 ,
, ,
,
(1)求 的值;
的值;
(2)若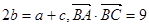 ,求
,求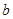 的值.
的值.
(本小题满分12分)
(1)已知函数f(x)=2x-x2,问方程f(x)=0在区间[-1,0]内是否有解,为什么?
(2)若方程ax2-x-1=0在(0,1)内恰有一解,求实数a的取值范围.
(本小题满分12分)
已知函数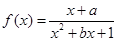 是奇函数:
是奇函数:
(1)求实数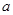 和
和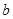 的值;
的值;
(2)证明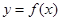 在区间
在区间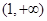 上的单调递减
上的单调递减
(3)已知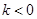 且不等式
且不等式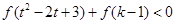 对任意的
对任意的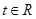 恒成立,求实数
恒成立,求实数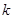 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 的定义域为
的定义域为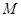 ,
,
(1)求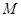 ;
;
(2)当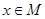 时,求函数
时,求函数 的最大值。
的最大值。
(本小题满分12分)
已知函数 。
。
(1)求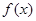 的振幅和最小正周期;
的振幅和最小正周期;
(2)求当 时,函数
时,函数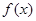 的值域;
的值域;
(3)当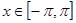 时,求
时,求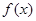 的单调递减区间。
的单调递减区间。