甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)求甲、乙两人考试均合格的概率;
(Ⅱ)求甲答对试题数 的概率分布.
的概率分布.
(本小题满分12分)某上市股票在30天内每股的交易价格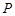 (元)与时间
(元)与时间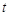 (天)组成有序数对
(天)组成有序数对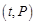 ,点
,点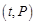 落在图中的两条线段上;该股票在30天内的日交易量
落在图中的两条线段上;该股票在30天内的日交易量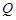 (万股)与时间
(万股)与时间 (天)的部分数据如下表所示
(天)的部分数据如下表所示
第 天 天 |
4 |
10 |
16 |
22 |
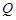 (万股) (万股) |
36 |
30 |
24 |
18 |
(1)根据提供的图像,写出该种股票每股交易价格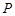 (元)与时间
(元)与时间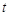 (天)所满足的函数关系式;
(天)所满足的函数关系式;
(2)根据表中数据,写出日交易量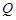 (万股)与时间
(万股)与时间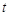 (天)的一次函数关系式;
(天)的一次函数关系式;
(3)用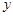 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出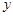 关于
关于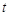 的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
(本小题满分12分)已知函数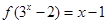
 ,将函数
,将函数 的图像向右平移2个单位,再向上平移3个单位可得函数
的图像向右平移2个单位,再向上平移3个单位可得函数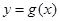 的图像.
的图像.
(1)求函数 与
与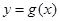 的解析式;
的解析式;
(2)设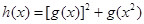 ,试求函数
,试求函数 的最值.
的最值.
( 本小题满分12分)已知 ,
,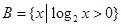 .
.
(1)求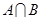 和
和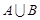 ;
;
(2)定义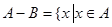 且
且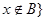 ,求
,求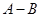 和
和 .
.
(本小题10分)
(1)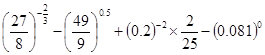
(2)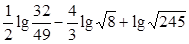
(本小题满分10分)某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下: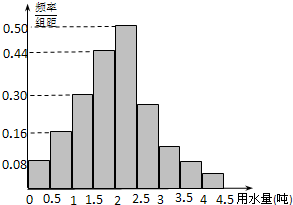
| 分组 |
频数 |
| [0,0.5) |
4 |
| [0.5,1) |
8 |
| [1,1.5) |
15 |
| [1.5,2) |
22 |
| [2,2.5) |
25 |
| [2.5,3) |
14 |
| [3,3.5) |
6 |
| [3.5,4) |
4 |
| [4,4.5] |
2 |
| 合计 |
100 |
(1)根据频率分布直方图估计这组数据的众数与平均数;
(2)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?