(本小题满分13分)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线L在y轴上的截距为m(m≠0),L交椭圆于A、B两个不同点。
(1)求椭圆的方程;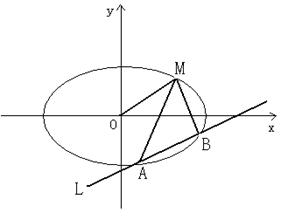
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形。
已知:函数f(x)= +lg(3
+lg(3 -9)的定义域为A,集合B=
-9)的定义域为A,集合B= ,
,
(1)求:集合A;
(2)求:A B。
B。
(本小题满分10分)
对于在区间 上有意义的两个函数
上有意义的两个函数 和
和 ,如果对于任意的
,如果对于任意的 ,都有
,都有 ,则称
,则称 与
与 在区间
在区间 上是“接近”的两个函数,否则称它们在
上是“接近”的两个函数,否则称它们在 上是“非接近”的两个函数。现有两个函数
上是“非接近”的两个函数。现有两个函数 ,给定一个区间
,给定一个区间 。
。
(1)若 与
与 在区间
在区间 都有意义,求实数
都有意义,求实数 的取值范围;
的取值范围;
(2)讨论 与
与 在区间
在区间 上是否是“接近”的两个函数。
上是否是“接近”的两个函数。
(本小题满分10分)
已知:向量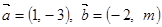 ,且
,且 。
。
(1)求实数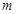 的值;
的值;
(2)当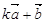 与
与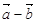 平行时,求实数
平行时,求实数 的值。
的值。
(本小题满分10分)
已知:向量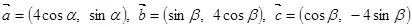
(1)若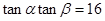 ,求证:
,求证: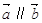 ;
;
(2)若 垂直,求
垂直,求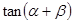 的值;
的值;
(3)求 的最大值。
的最大值。
(本小题满分10分)
已知:函数
(1)若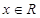 ,求函数
,求函数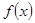 的最小正周期及图像的对称轴方程;
的最小正周期及图像的对称轴方程;
(2)设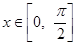 ,
,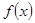 的最小值是-2,最大值是
的最小值是-2,最大值是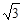 ,求:实数
,求:实数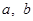 的值。
的值。