(本小题满分12分)已知函数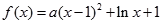 .
.
(Ⅰ)当 时,求函数
时,求函数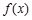 的极值;
的极值;
(Ⅱ)若函数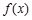 在区间
在区间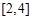 上是减函数,求实数a的取值范围;
上是减函数,求实数a的取值范围;
(Ⅲ)当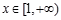 时,函数
时,函数 图象上的点都在
图象上的点都在 所表示的平面区域内,求数a的取值范围
所表示的平面区域内,求数a的取值范围
已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为 时,求弦AB的长.
时,求弦AB的长.
一圆与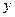 轴相切,圆心在直线
轴相切,圆心在直线 上,在
上,在 上截得的弦长为
上截得的弦长为 ,求此圆的方程.
,求此圆的方程.
已知长方形的四个顶点A(0,0)、B(2,0)、C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1<x4<2,求tanθ的取值范围.
已知:两点A ,B(3,2),过点P(2,1)的直线l与线段AB有公共点求直线l的倾斜角的取值范围
,B(3,2),过点P(2,1)的直线l与线段AB有公共点求直线l的倾斜角的取值范围
已知直线 与直线
与直线 没有公共点,
没有公共点,
求实数m的值