(本小题满分14分)已知函数 (
( ).
).
(1)若 为函数
为函数 的极值点,求
的极值点,求 的值;
的值;
(2)若 ,
, 已知
已知
 ,
,
 ,若直线
,若直线 、
、 及直线
及直线 与函数
与函数 的图象所围成的封闭图形如阴影部分所示,求阴影面积
的图象所围成的封闭图形如阴影部分所示,求阴影面积 关于
关于 的函数
的函数 的最小值
的最小值 ;
; 证明不等式:
证明不等式: .
.
函数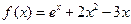 .
.
(1)求证函数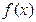 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应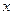 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
,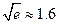 ,
, )
)
(2)当 时,若关于
时,若关于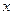 的不等式
的不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
(本小题满分13分)
若数列{an}的前n项和Sn是(1+x)n二项展开式中各项系数的和(n=1,2,3,……).
⑴求{an}的通项公式;
⑵若数列{bn}满足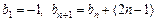 ,且
,且 ,求数列{cn}的通项及其前n项和Tn.
,求数列{cn}的通项及其前n项和Tn.
⑶求证: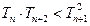 .
.
(本小题满分l2分)
在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分.已知某选手回答A、B、C三道题正确的概率分别为 、
、 、
、 ,且回答各题时相互之间没有影响.
,且回答各题时相互之间没有影响.
(1) 若此选手可以自由选择答题顺序,求其必答题总分为50分的概率;
(2) 若此选手按A、B、C的顺序答题,求其必答题总分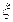 的分布列和数学期望.
的分布列和数学期望.
已知向量
(1)若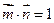 ,求
,求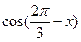 的值;
的值;
(2)记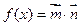 ,在
,在 中,角
中,角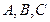 的对边分别是
的对边分别是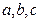 ,且满足
,且满足 ,求函数
,求函数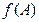 的取值范围。
的取值范围。
已知函数 将
将 的图象向右平移2个单位,得到
的图象向右平移2个单位,得到 的图象.
的图象.
(1)求函数 的解析式;
的解析式;
(2) 若函数 与函数
与函数 的图象关于直线
的图象关于直线 对称,求函数
对称,求函数 的解析式;
的解析式;
(3)设 已知
已知 的最小值是
的最小值是 ,且
,且 求实数
求实数 的
的 取值范围.
取值范围.