函数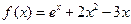
．
（1）求证函数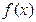
在区间
上存在唯一的极值点，并用二分法求函数取得极值时相应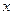
的近似值（误差不超过
）；（参考数据
，
，
）
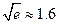（2）当
时，若关于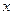的不等式
恒成立，试求实数
的取值范围.
选修4—4：坐标系与参数方程
已知直线l的参数方程为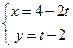
（t为参数），
P是椭圆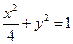
上任意一点，求点P到直线l距离的最大值.
选修4—1：几何证明选讲
如图，已知四边形ABCD内接于⊙O，EF//CD，FG切⊙O于点G.
求证EF=FG.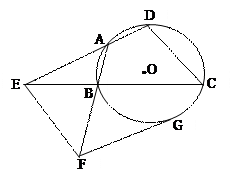
已知函数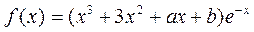
（I）如
，求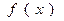
的单调区间；
（II）若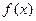
在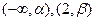
单调增加，在
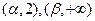单调减少，
证明
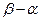＜6.
过抛物线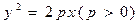
的对称轴上一点
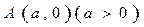的直线与抛物线相交于M、N两点，自M、N向直线
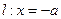作垂线，垂足分别为
、
。
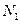（Ⅰ）当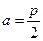
时，求证：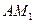
⊥
；
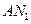（Ⅱ）记
、
、
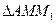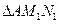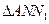的面积分别为
、
、
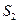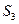，是否存在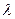
，使得对任意的
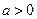，都有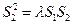
成立。若存在，求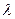值；若不在，说明理由。
如图，在三棱锥
中
底面
点
，
分别在棱
上，且
（Ⅰ）求证：
平面
；
（Ⅱ）当为
的中点时，求
与平面所成的角的大小；
（Ⅲ）是否存在点使得二面角
为直二面角？并说明理由.