(本小题满分l2分)
在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分.已知某选手回答A、B、C三道题正确的概率分别为 、
、 、
、 ,且回答各题时相互之间没有影响.
,且回答各题时相互之间没有影响.
(1) 若此选手可以自由选择答题顺序,求其必答题总分为50分的概率;
(2) 若此选手按A、B、C的顺序答题,求其必答题总分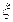 的分布列和数学期望.
的分布列和数学期望.
将一颗正方体的骰子先后抛掷2次(每个面朝上等可能),记下向上的点数,求:
(1)求两点数之和为5的概率;
(2)以第一次向上点数为横坐标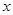 ,第二次向上的点数为纵坐标
,第二次向上的点数为纵坐标 的点
的点 在圆
在圆 的内部的概率.
的内部的概率.
在平面直角坐标系 中,已知圆
中,已知圆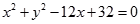 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 相交于不同的两点
相交于不同的两点 .
.
(1)求 的取值范围;
的取值范围;
(2)当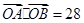 时,求直线
时,求直线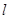 方程.
方程.
(3)在y轴上是否存在一点C,使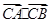 是定值,若存在求C坐标并求此时
是定值,若存在求C坐标并求此时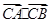 的值,若不存在说明理由.
的值,若不存在说明理由.
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若OM=ON,求圆C的方程;
某高中有高级教师96人,中级教师144人,初级教师48人,为了进一步推进高中课程改革,邀请甲、乙、丙、丁四位专家到校指导。学校计划从所有教师中采用分层抽样办法选取6名教师分别与专家一对一交流,选出的6名教师再由专家随机抽取教师进行教学调研。
(1)求应从高级教师、中级教师、初级教师中分别抽取几人;
(2)若甲专家选取了两名教师,这两名教师分别是高级教师和中级教师的概率;
(3)若每位专家只抽一名教师,每位教师只与其中一位专家交流,求高级教师恰有一人被抽到的概率。
有A、B、C、D、E五位工人参加技能竞赛培训.现分别从A、B二人在培训期间参加的若干次预赛成绩中随机抽取8次.
用右侧茎叶图表示这两组数据:
(1)A、B二人预赛成绩的中位数分别是多少?
(2)现要从A、B中选派一人参加技能竞赛,从平均状况和方差的角度考虑,你认为派哪位工人参加合 适?请说明理由;
(3)若从参加培训的5位工人中选2人参加技能竞赛,求A、B二人中至少有一人参加技能竞赛的概率.