将一颗正方体的骰子先后抛掷2次(每个面朝上等可能),记下向上的点数,求:
(1)求两点数之和为5的概率;
(2)以第一次向上点数为横坐标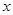 ,第二次向上的点数为纵坐标
,第二次向上的点数为纵坐标 的点
的点 在圆
在圆 的内部的概率.
的内部的概率.
如图在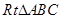 中,三个顶点坐标分别为
中,三个顶点坐标分别为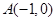 ,
, ,
,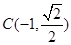 ,曲线
,曲线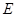 过
过 点且曲线
点且曲线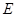 上任一点
上任一点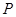 满足
满足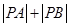 是定值.
是定值.
(Ⅰ)求出曲线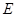 的标准方程;
的标准方程;
(Ⅱ)设曲线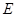 与
与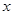 轴,
轴, 轴的交点分别为
轴的交点分别为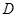 、
、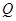 ,
,
是否存在斜率为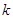 的直线
的直线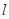 过定点
过定点 与曲线
与曲线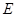 交于不同的两点
交于不同的两点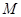 、
、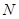 ,且向量
,且向量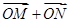 与
与 共线.若存在,求出此直线方程;若不存在,请说明理由.
共线.若存在,求出此直线方程;若不存在,请说明理由.
如图,四棱锥 中,底面
中,底面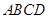 为矩形,
为矩形, 底面
底面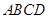 ,且
,且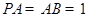 ,
,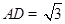 ,点
,点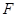 是
是 中点.
中点.
(Ⅰ)若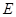 为
为 中点,证明:
中点,证明: //平面
//平面 ;
;
(Ⅱ)若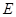 是
是 边上任一点,证明:
边上任一点,证明: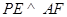 ;
;
(Ⅲ)若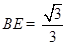 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.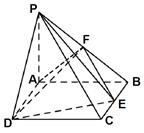
如图为一建筑物的正视图,尺寸图中标出,为了做好火灾的防备工作,需要在地面上确定安装喷水枪的地点 ,经测试只有当
,经测试只有当 (图中的
(图中的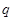 角)时,才能使得水枪喷射能够覆盖整个建筑物,求水枪安装点
角)时,才能使得水枪喷射能够覆盖整个建筑物,求水枪安装点 到建筑物的距离
到建筑物的距离 长.(注:图中
长.(注:图中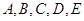 在同一个平面内;不考虑喷水枪的高度.)
在同一个平面内;不考虑喷水枪的高度.)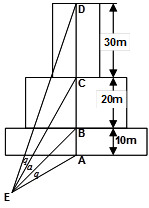
已知数列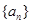 是首项
是首项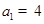 ,公比
,公比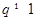 的等比数列,
的等比数列, 是其前
是其前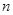 项和,且
项和,且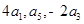 成等差数列.
成等差数列.
(Ⅰ)求公比 的值;
的值;
(Ⅱ)设 ,求
,求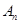 的值.
的值.
已知函数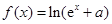 (
( 为常数)是
为常数)是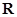 上的奇函数,函数
上的奇函数,函数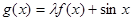 是区间
是区间 上的减函数.
上的减函数.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 上恒成立,求
上恒成立,求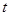 的取值范围;
的取值范围;
(Ⅲ)讨论关于 的方程
的方程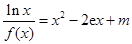 的根的个数。
的根的个数。