如图为一建筑物的正视图,尺寸图中标出,为了做好火灾的防备工作,需要在地面上确定安装喷水枪的地点 ,经测试只有当
,经测试只有当 (图中的
(图中的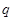 角)时,才能使得水枪喷射能够覆盖整个建筑物,求水枪安装点
角)时,才能使得水枪喷射能够覆盖整个建筑物,求水枪安装点 到建筑物的距离
到建筑物的距离 长.(注:图中
长.(注:图中 在同一个平面内;不考虑喷水枪的高度.)
在同一个平面内;不考虑喷水枪的高度.)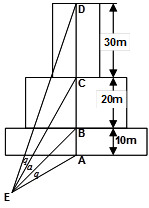
已知椭圆 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线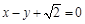 相切.
相切.
(1)求椭圆C的方程;
(2)设 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 于另一点
于另一点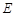 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;
(3)在(2)的条件下,证明直线 与
与 轴相交于定点.
轴相交于定点.
在直角坐标系中,射线OA: x-y=0(x≥0),
OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.
(1)当AB中点为P时,求直线AB的方程;
(2)当AB中点在直线 上时,求直线AB的方程.
上时,求直线AB的方程.
已知四棱锥P-ABCD的直观图(如图(1))及左视图(如图(2)),底面ABCD是边长为2的正方形,平面PAB⊥平面ABCD,PA=PB。
(1)求证:AD⊥PB;
(2)求异面直线PD与AB所成角的余弦值;
(3)求平面PAB与平面PCD所成锐二面角的大小.
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为
(1)求双曲线C的方程;
(2)若直线 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 (其中O为原点). 求k的取值范围.
(其中O为原点). 求k的取值范围.
如图,矩形 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且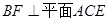 ,AC、BD交于点G.
,AC、BD交于点G.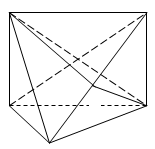
(1)求证: ;
;
(2)求证; ;
;
(3)求三棱锥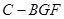 的体积.
的体积.