已知四棱锥P-ABCD的直观图(如图(1))及左视图(如图(2)),底面ABCD是边长为2的正方形,平面PAB⊥平面ABCD,PA=PB。
(1)求证:AD⊥PB;
(2)求异面直线PD与AB所成角的余弦值;
(3)求平面PAB与平面PCD所成锐二面角的大小.
甲、乙两人各射击3次,甲每次击中目标的概率为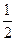 ,乙每次击中目标的概率为
,乙每次击中目标的概率为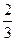 ,
,
(1)记甲击中目标的次数为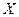 ,求随机变量
,求随机变量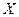 的概率分布表及数学期望
的概率分布表及数学期望 ;
;
(2)求乙至多击中目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率.
若
 展开式中前三项系数成等差数列,
展开式中前三项系数成等差数列,
(1)求 的值;
的值;
(2)求展开式中第4项的系数和二项式系数;
(3)求展开式中 的一次项.
的一次项.
如图,在直三棱柱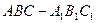 中,
中, ,点
,点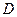 是
是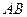 的中点,
的中点,
(1)求证: 平面
平面
(2)求证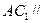 平面
平面
 |
有3本不同的语文书和3本不同的数学书,求满足下列条件的方法总数(用数字作答)
(1)6本排成一排;
(2)6本排成一排,其中3本数学书必须相邻;
(3)6本排成一排,其中语文书互不相邻.
在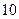 件产品中,有
件产品中,有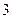 件一等品,
件一等品,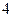 件二等品,
件二等品,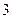 件三等品,从这
件三等品,从这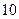 件产品中任取
件产品中任取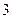 件
件
求:(1)取出的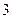 件产品中一等品的件数
件产品中一等品的件数 的分布列和数学期望
的分布列和数学期望
(2)取出的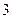 件产品中一等品的件数多余二等品件数的概率
件产品中一等品的件数多余二等品件数的概率