在平面直角坐标系 中,已知圆
中,已知圆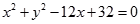 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 相交于不同的两点
相交于不同的两点 .
.
(1)求 的取值范围;
的取值范围;
(2)当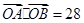 时,求直线
时,求直线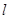 方程.
方程.
(3)在y轴上是否存在一点C,使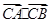 是定值,若存在求C坐标并求此时
是定值,若存在求C坐标并求此时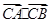 的值,若不存在说明理由.
的值,若不存在说明理由.
中心在原点,一焦点为F1(0,5 )的椭圆被直线y=3x-2截得的弦的中点横坐标是
)的椭圆被直线y=3x-2截得的弦的中点横坐标是 ,求此椭圆的方程。
,求此椭圆的方程。
椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.
已知三角形 的两顶点为
的两顶点为 ,它的周长为
,它的周长为 ,求顶点
,求顶点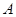 轨迹方程.
轨迹方程.
设P,Q,R,S四人分比获得1——4等奖,已知:
(1)若P得一等奖,则Q得四等奖;
(2)若Q得三等奖,则P得四等奖;
(3)P所得奖的等级高于R;
(4)若S未得一等奖,则P得二等奖;
(5)若Q得二等奖,则R不是四等奖;
(6)若Q得一等奖,则R得二等奖。
问P,Q,R,S分别获得几等奖?
写出下列各命题的否命题和命题的否定:
(1) ,若
,若 ,则
,则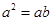 ;
;
(2)若 ,则
,则 ;
;
(3)若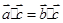 ,则
,则 ;
;
(4)若 ,则
,则 是等比数列。
是等比数列。