设函数 ,其中
,其中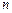 为正整数.
为正整数.
(1)判断函数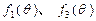 的单调性,并就
的单调性,并就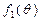 的情形证明你的结论;
的情形证明你的结论;
(2)证明: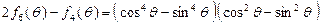 ;
;
(3)对于任意给定的正整数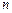 ,求函数
,求函数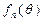 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)定义在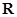 上的函数
上的函数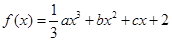 同时满足以下条件:
同时满足以下条件:
①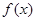 在
在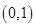 上是减函数,在
上是减函数,在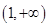 上是增函数;
上是增函数;
②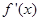 是偶函数;
是偶函数;
③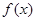 在
在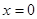 处的切线与直线
处的切线与直线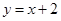 垂直.
垂直.
(1)求函数 的解析式;
的解析式;
(2)设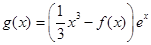 ,求函数
,求函数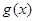 在
在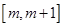 上的最小值.
上的最小值.
.(本小题满分12分)已知椭圆的中心在原点,焦点在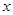 轴上,一个顶点为
轴上,一个顶点为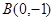 ,且其右焦点到直线
,且其右焦点到直线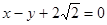 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)是否存在斜率为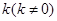 ,且过定点
,且过定点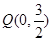 的直线
的直线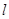 ,使
,使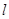 与椭圆交于两个不同的点
与椭圆交于两个不同的点 、
、 ,且
,且 ?若存在,求出直线
?若存在,求出直线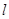 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)如图,在四面体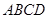 中,
中, ,
,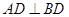 ,点
,点 ,
,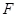 分别是
分别是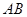 ,
, 的中点.
的中点.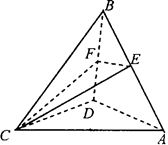
(1)求证:平面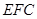 ⊥平面
⊥平面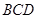 ;
;
(2)若平面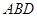 ⊥平面
⊥平面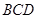 ,且
,且 ,求三棱锥
,求三棱锥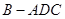 的体积.
的体积.
(本小题满分12分)有A、B、C、D、E五位工人参加技能竞赛培训.现分别从A、B二人在培训期间参加的若干次预赛成绩中随机抽取8次.用茎叶图表示这两组数据如下: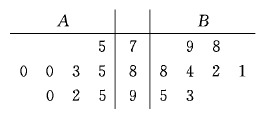
(1)现要从A、B中选派一人参加技能竞赛,从平均状况和方差的角度考虑,你认为派哪位工人参加合适?请说明理由;
(2)若从参加培训的5位工人中选2人参加技能竞赛,求A、B二人中至少有一人参加技能竞赛的概率.
(本小题满分12分) 锐角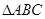 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为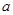 、
、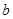 、
、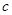 ,且
,且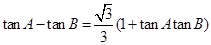 .
.
(1)若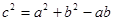 ,求角A、B、C大小;
,求角A、B、C大小;
(2)已知向量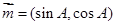 ,
,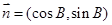 ,求
,求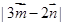 的取值范围.
的取值范围.