．甲、乙两射击运动员进行射击比赛，射击次数相同，已知两运动员击中的环数
稳定在7，8，
9，10环，他们比赛成绩的频率分布
直方图如下：（如果将频率近似的看作概率）
（1）估计乙运动员击中8环的概率，并求甲、乙同时击中9环以上（包括9环）的概率；
（2）求甲运动员击中环数的概率分布列及期望；若从甲、乙运动员中只能挑选一名参加某大型比赛，你认为让谁参加比较合适？
如图，在直三棱柱
中， AB=1，
，
.
(Ⅰ)证明：
；
（Ⅱ）求二面角A—
—B的余弦值。
已知命题
：“函数
在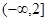
上单调递减”，命题
：“
，
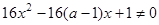”，若命题“且”为真命题，求实数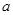
的取值范围.
在长方体
中，已知DA=DC=4,DD1=3,求异面直线A1B与B1C所成角的余弦值。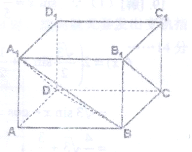
(本小题满分12分)已知椭圆：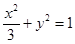
，过坐标原点O作两条互相垂直的射线，与椭圆分别交于A，B两点．
(I)求证O到直线AB的距离为定值．
(Ⅱ)求△0AB面积的最大值．
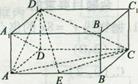
(本小题满分12分)如图，在长方体ABCD-A1B1C1D1中，AD=AAl=1，AB=2，点E在棱AB上移动．
(I)证明：D1E上AlD；
(Ⅱ)当E为AB的中点时，求点E到面ACD1的距离；
(Ⅲ)在(II)的条件下，求D1E与平面AD1C所成角的正弦值．