设α,β是方程x2-ax+b=0的两个实根,试分析a>2且b>1是两根α、β均大于1的什么条件?
已知函数 在区间
在区间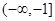 上是增函数,求
上是增函数,求 的取值范围
的取值范围
已知函数f(x),x∈R,满足①f(1+x)=f(1-x),②在[1,+∞]上为增函数,③x1<0,x2>0且x1+x2<-2,试比较f(-x1)与f(-x2)的大小关系.
已知函数f(x)=2x2+bx可化为f(x)=2(x+m)2-4的形式.其中b>0.求f(x)为增函数的区间.
已知二次函数f(x)=a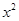 +bx(a,b是常数且a
+bx(a,b是常数且a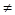 0)满足条件:f(2)=0.方程f(x)=x有等根
0)满足条件:f(2)=0.方程f(x)=x有等根
(1)求f(x)的解析式;
(2)问:是否存在实数m,n使得f(x)定义域和值域分别为[m,n]和
[2m,2n],如存在,求出m,n的值;如不存在,说明理由.
已知函数f(x)=2(m-1)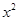 -4mx+2m-1
-4mx+2m-1
(1)m为何值时,函数图像与x轴有一个公共点.
(2)如果函数的一个零点为2,求m的值.