已知倾斜角为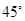 的直线
的直线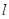 过点
过点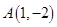 和点
和点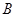 ,点
,点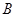 在第一象限,
在第一象限,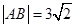 。
。
(1)求点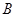 的坐标;
的坐标;
(2)若直线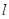 与双曲线
与双曲线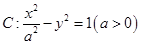 相交于
相交于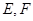 两点,且线段
两点,且线段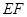 的中点坐标为
的中点坐标为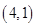 ,求
,求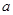 的值;
的值;
(3)对于平面上任一点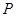 ,当点
,当点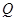 在线段
在线段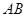 上运动时,称
上运动时,称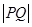 的最小值为
的最小值为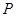 与线段
与线段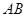 的距离。已知
的距离。已知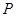 在
在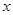 轴上运动,写出点
轴上运动,写出点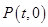 到线段
到线段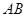 的距离
的距离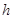 关于
关于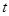 的函数关系式。
的函数关系式。
(本小题满分l0分)计算下列定积分
(1)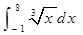 (2)
(2)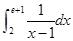
已知数列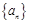 是各项均不为
是各项均不为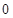 的等差数列,公差为
的等差数列,公差为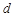 ,
,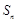 为其前
为其前 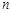 项和,且满足
项和,且满足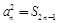 ,
,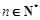 .数列
.数列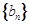 满足
满足 ,
,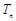 为数列
为数列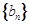 的前n项和.
的前n项和.
(1)求数列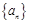 的通项公式
的通项公式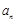 和数列
和数列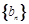 的前n项和
的前n项和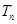 ;
;
(2)若对任意的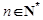 ,不等式
,不等式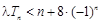 恒成立,求实数
恒成立,求实数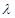 的取值范围;
的取值范围;
(3)是否存在正整数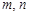
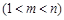 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有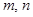 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
在等差数列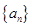 中,
中,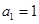 ,前
,前 项和
项和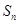 满足条件
满足条件 ,
,
(Ⅰ)求数列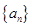 的通项公式;
的通项公式;
(Ⅱ)记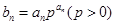 ,求数列
,求数列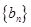 的前
的前 项和
项和 。
。
建造一间地面面积为12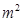 的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/
的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/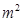 , 侧面的造价为80元/
, 侧面的造价为80元/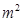 , 屋顶造价为1120元. 如果墙高3
, 屋顶造价为1120元. 如果墙高3 , 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元?
, 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元?
在△ABC中,角A、B、C所对应的边为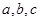
(1)若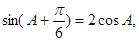 求A的值;
求A的值;
(2)若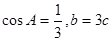 ,求
,求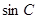 的值.
的值.