设m是实数,记M={m|m>1},f(x)=log3(x2-4mx+4m2+m+ )
)
(1)证明: 当m∈M时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x都有意义,则m∈M。
(2)当m∈M时,求函数f(x)的最小值。
(3)求证: 对每个m∈M,函数f(x)的最小值都不小于1。
不等式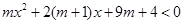 的解集为
的解集为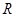 ,求实数
,求实数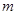 的取值范围
的取值范围
在△ABC中,已知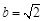 ,c=1,
,c=1,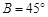 ,求a,A,C.
,求a,A,C.
已知等差数列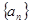 中
中
(1)求数列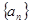 的通项公式
的通项公式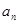
(2)当n取何值时,数列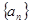 的前
的前 项和
项和 取得最值 ,并求出最值。
取得最值 ,并求出最值。
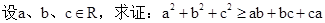
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元。
(1).当一次订购量为多少个时,零件的实际出厂单价恰降为51元;
(2).设一次订购量为 个,零件的实际出厂单价为
个,零件的实际出厂单价为 元,写出函数
元,写出函数 的解析式;
的解析式;
(3).当销售商一次订购500个零件时,该厂获得的利润是多少元?如果一次订购1000个零件时,该厂获得的利润又是多少元?